
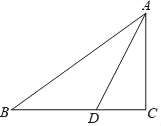
【题目】如图,在△ABC中,∠C=90°,AD平分∠BAC,
(1)求作⊙O,圆心O是AD的中垂线与AB的交点,OD为半径.(尺规作图,不写作法,保留痕迹)
(2)求证:BC是⊙O切线.
(3)若BD=5,DC=3,求AC的长.
【答案】(1)作图见解析;(2)证明见解析;(3)6.
【解析】
(1)由中垂线的尺规作图得到点O,再作圆即可;
(2)要证BC是⊙O的切线,只要连接OD,再证OD⊥BC即可.
(3)过点D作DE⊥AB,根据角平分线的性质可知CD=DE=3,由勾股定理得到BE的长,再通过证明△BDE∽△BAC,根据相似三角形的性质得出AC的长.
解:(1)如图,⊙O即为所求;
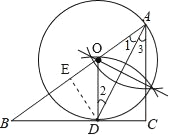
(2)∵AD是∠BAC的平分线,
∴∠1=∠3.
∵OA=OD,
∴∠1=∠2.
∴∠2=∠3.
∴OD∥AC,
∴∠ODB=∠ACB=90°.
∴OD⊥BC.
∴BC是⊙O切线.
(3)过点D作DE⊥AB,
∵AD是∠BAC的平分线,
∴CD=DE=3.
在Rt△BDE中,∠BED=90°,
由勾股定理得: ![]()
∵∠BED=∠ACB=90°,∠B=∠B,
∴△BDE∽△BAC.
∴![]()
∴![]()
∴AC=6.


科目:初中数学 来源: 题型:
【题目】如图,在等腰三角形ABC中,∠ABC=90°,D为AC边上中点,过D点作DE⊥DF,交AB于E,交BC于F,若S四边形BFDE=9,则AB的长为:
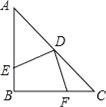
A. 3 B. 6 C. 9 D. 18
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边周长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边长为x米.
(1)若苗圃园的面积为72平方米,求x;
(2)若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由;
(3)当这个苗圃园的面积不小于100平方米时,直接写出x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD中,AB=6,BC=2,直线l是长方形ABCD的一条对称轴,且分别与AD,BC交于点E,F,若直线l上的动点P,使得△PAB和△PBC均为等腰三角形.则动点P的个数有_______个.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在△ABC中,AB=AC,D是BC的中点,动点E在边AB上(点E不与点A,B重合), 动点F在射线AC上,连结DE, DF.
(1)如图1,当∠DEB=∠DFC=90°时,直接写出DE与DF的数量关系;

(2)如图2,当∠DEB+∠DFC=180°(∠DEB≠∠DFC)时,猜想DE与DF的数量关系,并证明;

(3)当点E,D,F在同一条直线上时,
①依题意补全图3;
②在点E运动的过程中,是否存在EB=FC? ( 填“存在”或“不存在” ).

查看答案和解析>>
科目:初中数学 来源: 题型:
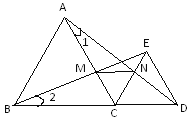
【题目】如图,点C为线段BD上的点,分别以BC,CD为边作等边三角形ABC和等边三角形ECD,连接BE交AC于点M,连接AD交CE于点N,连接MN.试说明:(1)![]() ;(2)
;(2)![]() 为等边三角形.
为等边三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,正方体盒子的棱长为2,BC的中点为M.
(1)一只蚂蚁从点M沿正方体的棱爬到点D1,蚂蚁爬行的最短路程是多少?
(2)若蚂蚁从点M沿正方体的表面爬行到点D1,请你结合正方体的展开图画出蚂蚁爬行的最短路线.

查看答案和解析>>
科目:初中数学 来源: 题型:
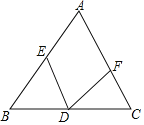
【题目】如图,已知在△ABC中,AB=AC,D为BC上一点,BE=CD,CF=BD,那么∠EDF等于( )
A.90°﹣∠AB.90°﹣![]() ∠AC.45°﹣
∠AC.45°﹣![]() ∠AD.180°﹣∠A
∠AD.180°﹣∠A
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是⊙O的内接三角形,AB=AC,∠BCA=65°,作CD∥AB,并与○O相交于点D,连接BD,则∠DBC的大小为

A. 15° B. 35° C. 25° D. 45°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com