
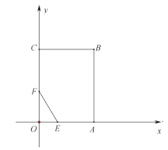
【题目】如图,在平面直角坐标系中,矩形![]() 的顶点
的顶点![]() 、
、![]() 分别落在
分别落在![]() 轴、
轴、![]() 轴正半轴上,点
轴正半轴上,点![]() 在边
在边![]() 上,点
上,点![]() 在边
在边![]() 上,且
上,且![]() ,已知
,已知![]() ,
,![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)点![]() 关于点
关于点![]() 的对称点为点
的对称点为点![]() ,点
,点![]() 从
从![]() 点出发,以每秒1个单位的速度沿射线
点出发,以每秒1个单位的速度沿射线![]() 运动,设
运动,设![]() 点的运动时间为
点的运动时间为![]() 秒,
秒,![]() 的面积为
的面积为![]() ,用含
,用含![]() 的代数式表示
的代数式表示![]() ;
;
(3)在(2)的条件下,点![]() 为平面内一点,点
为平面内一点,点![]() 在线段
在线段![]() 上运动时,作
上运动时,作![]() 的平分线交
的平分线交![]() 轴于点
轴于点![]() ,
,![]() 为何值时,四边形
为何值时,四边形![]() 为矩形?并求此时点
为矩形?并求此时点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)
;(2)![]()
![]() ;(3)故当t=4时,四边形
;(3)故当t=4时,四边形![]() 为矩形,此时M(6,-3).
为矩形,此时M(6,-3).
【解析】
(1)先确定出点A的坐标,进而得出OA,最后在Rt△OEF中,利用勾股定理求出OE即可得出点E的坐标;
(2)分两种情况,用三角形的面积公式即可解决问题;
(3)先利用对称求出点D的坐标,进而得出OD,由角平分线的性质定理得出DP=OD求出点P的坐标,再利用勾股定理求出点N的坐标,根据矩形的性质,由点的平移方式即可求得点M的坐标.
解:(1)在矩形OABC中,B(6,8),
∴A(6,0),
∴OA=6,
设OE=a,
∴EF=AE=OA-OE=6-a,
∵![]() ,
,
![]() ,
,
在Rt△AEF中,根据勾股定理得,OE2+OF2=EF2,
∴a2+12=(6-a)2,
∴![]() ,
,
∴![]() ;
;
(2)∵BC∥OA,B(6,8),OC=AB=8,
∴P(t,8),PB=|t-6|
①当点P在边BC上时,如图1,
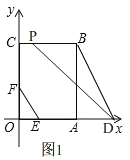
∴0≤t<6,
∴PB=6-t,
![]() ;
;
②当点P在CB的延长时,如图2,

∴t>6,
∴PB=t-6,
![]() ,
,
即:![]() ;
;
(3)由(1)知,![]() ,
,
∴![]() ,
,
∵点D是点E关于点A的对称点,
∴![]() ,
,
∴![]() ,
,
如图3,
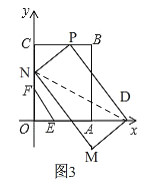
∵四边形DPNM是矩形,
∴∠DPN=90°=∠DON,
∴NP⊥DP,NO⊥OD,
∵DN是∠PDO的平分线,
∴NO=NP,
在Rt△NDO和Rt△NDP中,
![]() ,
,
∴Rt△NDO≌Rt△NDP(HL),
∴![]() ,
,
∵P(t,8),![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() (点P在线段BC上,舍去)
(点P在线段BC上,舍去)
∴P(4,8)
设N(0,n),
∴ON=n,
∴PN=n,CN=OC-ON=8-n,
在Rt△CNP中,根据勾股定理得,CN2+CP2=PN2,
∴(8-n)2+16=n2,
∴n=5,
∴N(0,5),
即点P(4,8)平移到N(0,5),向左平移四个单位,向下平移3个单位,
点D(10,0)由此方式平移后得到的M(6,-3).
故当t=4时,四边形![]() 为矩形,此时M(6,-3).
为矩形,此时M(6,-3).


科目:初中数学 来源: 题型:
【题目】光明电器超市销售每台进价分别为190元、160元的A、B两种型号的电风扇,下表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 2台 | 6台 | 1840元 |
第二周 | 5台 | 7台 | 2840 元 |
(进价、售价均保持不变,利润=销售收入-进货成本)
(1)求A、B两种型号的电风扇的销售单价;
(2)若超市准备再采购这两种型号的电风扇共40台,这40台电风扇全部售出后,若利润不低于2660元,求A种型号的电风扇至少要采购多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市计划购进甲、乙两种商品,已知甲的进价比乙多20元/件,用2000元购进甲种商品的件数与用1600元购进乙种商品的件数相同.
(1)求甲、乙两种商品的进价各是多少元?
(2)小丽用950元只购买乙种商品,她购买乙种商品件数y(件),该商品的销售单价x(元),列出y与x函数关系式?若超市销售乙种商品,至少要获得20%的利润,那么小丽最多可以购买多少件乙种商品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程:x2﹣(m﹣3)x﹣m=0
(1)证明原方程有两个不相等的实数根;
(2)若抛物线y=x2﹣(m﹣3)x﹣m与x轴交于A(x1,0),B(x2,0)两点,则A,B两点间的距离是否存在最大或最小值?若存在,求出这个值;若不存在,请说明理由.(友情提示:AB=|x1﹣x2|)
查看答案和解析>>
科目:初中数学 来源: 题型:
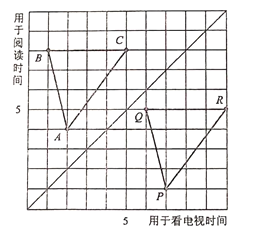
【题目】图中,点A,B,C,P,Q,R显示了6名学生平均每周用于阅读课外书的时间和用于看电视的时间(单位:h)
(1)用有序数对表示图中点A,B,C,P,Q,R
(2)图中方格纸的对角线的左上方的点有什么共同的特点?它右下方的点呢?
(3)三角形ABC的图形经过怎样的变换后得到三角形PQR的图形?其中点A对应点P,点B对应点Q,点C对应点R
查看答案和解析>>
科目:初中数学 来源: 题型:
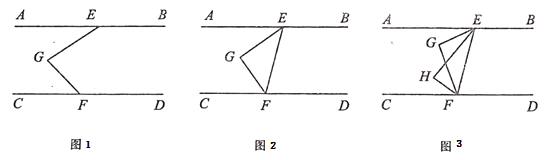
【题目】(1)如图1,已知AB∥CD,求证:∠EGF=∠AEG+∠CFG
(2)如图2,已知AB∥CD,∠AEF与∠CFE的平分线交于点G.猜想∠G的度数。证明你的猜想
(3)如图3,已知AB∥CD,EG平分∠AEH,EH平分∠GEF,FH平分∠CFG,FG平分∠HFE,∠G=95°,求∠H的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场以每件42元的价钱购进一种服装,根据试销得知:这种服装每天的销售量t(件),与每件的销售价x(元/件)可看成是一次函数关系:t=-3x+204.
(1)写出商场卖这种服装每天的销售利润![]() 与每件的销售价
与每件的销售价![]() 之间的函数关系式(每天的销售利润是指所卖出服装的销售价与购进价的差);
之间的函数关系式(每天的销售利润是指所卖出服装的销售价与购进价的差);
(2)通过对所得函数关系式进行配方,指出:商场要想每天获得最大的销售利润,每件的销售价定为多少最为合适;最大销售利润为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自2020年开始,新冠病毒疫情严峻,某爱心组织紧急筹集了部分资金,计划购买甲、乙两种救灾物品共4000件送往武汉,已知每件甲种物品的价格比每件乙种物品的价格贵10元,用450元购买甲种物品的件数恰好与用400元购买乙种物品的件数相同.
(1)求甲、乙两种救灾物品每件的价格分别是多少元?
(2)经调查,灾区对乙种物品件数需求量是甲种物品件数的3倍,若该爱心组织按照此需求的比例购买这4000件物品,需筹集资金多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
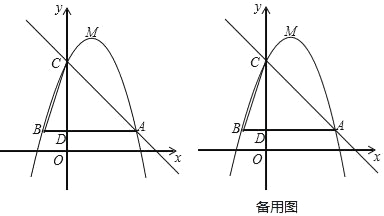
【题目】如图,已知二次函数y=﹣x2+bx+c(其中b,c为常数)的图象经过点A(3,1),点C(0,4),顶点为点M,过点A作AB∥x轴,交y轴于点D,交该二次函数图象于点B,连结BC.
(1)求该二次函数的解析式及点M的坐标.
(2)若将该二次函数图象向下平移m(m>0)个单位,使平移后得到的二次函数图象的顶点落在△ABC的内部(不包括△ABC的边界),求m的取值范围.
(3)沿直线AC方向平移该二次函数图象,使得CM与平移前的CB相等,求平移后点M的坐标.
(4)点P是直线AC上的动点,过点P作直线AC的垂线PQ,记点M关于直线PQ的对称点为M′.当以点P、A、M、M′为顶点的四边形为平行四边形时,直接写出点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com