
【题目】如图,已知二次函数y=﹣x2+bx+c(其中b,c为常数)的图象经过点A(3,1),点C(0,4),顶点为点M,过点A作AB∥x轴,交y轴于点D,交该二次函数图象于点B,连结BC.
(1)求该二次函数的解析式及点M的坐标.
(2)若将该二次函数图象向下平移m(m>0)个单位,使平移后得到的二次函数图象的顶点落在△ABC的内部(不包括△ABC的边界),求m的取值范围.
(3)沿直线AC方向平移该二次函数图象,使得CM与平移前的CB相等,求平移后点M的坐标.
(4)点P是直线AC上的动点,过点P作直线AC的垂线PQ,记点M关于直线PQ的对称点为M′.当以点P、A、M、M′为顶点的四边形为平行四边形时,直接写出点P的坐标.
【答案】(1)y=﹣x2+2x+4,(1,5);
(2)2<m<4;(3)(3,3)或(﹣1,7);(4)(1,3)或(﹣3,7).
【解析】试题分析:(1)利用待定系数法,求二次函数解析式.(2)先求出AC直线解析式,平移后顶点AC下方,AB上方,在求出坐标的范围.(3) 当y=1时,﹣x2+2x+4=1,解得x=﹣1或3,利用MM′∥AC,可得平移后的M的坐标.(4) 连接MC,MM′交PQ于F,设出各点坐标,则四边形CMFP是矩形, 当四边形 PAM′M是平行四边形时,分别求出P的坐标为(1,3)或(﹣3,7).
试题解析:
解:(1)把点A(3,1),点C(0,4)代入二次函数y=﹣x2+bx+c得
![]() ,解得
,解得![]() ,
,
∴二次函数解析式为y=﹣x2+2x+4,
配方得y=﹣(x﹣1)2+5,
∴点M的坐标为(1,5).
(2)设直线AC解析式为y=kx+b,把点A(3,1),C(0,4)代入得![]() ,
,
解得: ![]() ,
,
∴直线AC的解析式为y=﹣x+4,如图所示,对称轴直线x=1与△ABC两边分别交于点E、点F,
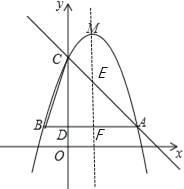
把x=1代入直线AC解析式y=﹣x+4解得y=3,则点E坐标为(1,3),点F坐标为(1,1),
点M向下平移m个单位后,坐标为(1,5﹣m),
由题意:1<5﹣m<3,解得2<m<4;
∴2<m<4.
(3)如图,
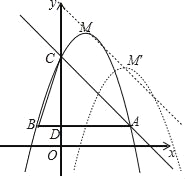
当y=1时,﹣x2+2x+4=1,解得x=﹣1或3,
∴B(﹣1,1),
∵C(0,4),
∴BC=![]() ,
,
∵MM′∥AC,CM′=![]() ,M(1,5),
,M(1,5),
∴M′的坐标为(3,3)或(﹣1,7),
∴平移后点M的坐标(3,3)或(﹣1,7).
(4)如图,连接MC,MM′交PQ于F,则四边形CMFP是矩形,
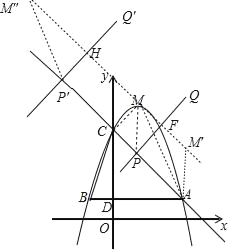
当四边形 PAM′M是平行四边形时,PA=MM′=2MF=2PC,设P(m,﹣m+4),
则有![]() (3﹣m)=2
(3﹣m)=2![]() m,
m,
∴m=1,
∴P(1,3),
当P′AMM′是平行四边形时,易知AP′=2CP′,
∴![]() (3﹣m)=2
(3﹣m)=2![]() (﹣m),
(﹣m),
解得m=﹣3,
∴P(﹣3,7),
综上所述,满足条件的点P的坐标为(1,3)或(﹣3,7).


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
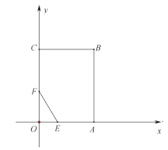
【题目】如图,在平面直角坐标系中,矩形![]() 的顶点
的顶点![]() 、
、![]() 分别落在
分别落在![]() 轴、
轴、![]() 轴正半轴上,点
轴正半轴上,点![]() 在边
在边![]() 上,点
上,点![]() 在边
在边![]() 上,且
上,且![]() ,已知
,已知![]() ,
,![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)点![]() 关于点
关于点![]() 的对称点为点
的对称点为点![]() ,点
,点![]() 从
从![]() 点出发,以每秒1个单位的速度沿射线
点出发,以每秒1个单位的速度沿射线![]() 运动,设
运动,设![]() 点的运动时间为
点的运动时间为![]() 秒,
秒,![]() 的面积为
的面积为![]() ,用含
,用含![]() 的代数式表示
的代数式表示![]() ;
;
(3)在(2)的条件下,点![]() 为平面内一点,点
为平面内一点,点![]() 在线段
在线段![]() 上运动时,作
上运动时,作![]() 的平分线交
的平分线交![]() 轴于点
轴于点![]() ,
,![]() 为何值时,四边形
为何值时,四边形![]() 为矩形?并求此时点
为矩形?并求此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利民商场经营某种品牌的T恤,购进时的单价是300元,根据市场调查:在一段时间内,销售单价是400元时,销售量是60件,销售单价每涨10元,销售量就减少1件.设这种T恤的销售单价为x元(x>400)时,销售量为y件、销售利润为W元.
(1)请分别用含x的代数式表示y和W(把结果填入下表):
销售单价(元) | x |
销售量y(件) | |
销售利润W(元) |
(2)该商场计划实现销售利润10000元,并尽可能增加销售量,那么x的值应当是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“书香长沙2019世界读书日”系列主题活动激发了学生的阅读兴趣,我校为满足学生的阅读需求,欲购进一批学生喜欢的图书,学校组织学生会成员随机抽取部分学生进行问卷调查,被调查学生须从“文史类、杜科类、小说类、生活类”中选择自己喜欢的一类,根据调查结果绘制了统计图(未完成),请根据图中信息,解答下列问题:
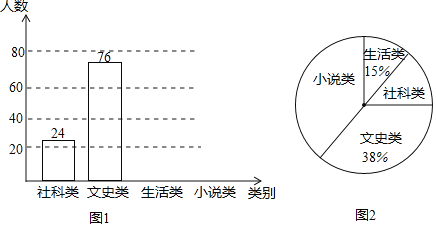
(1)此次共调查了 名学生;
(2)将条形统计图补充完整;
(3)图2中“小说类”所在扇形的圆心角为 度;
(4)若该校共有学生3000人,估计该校喜欢“文史类”书籍的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
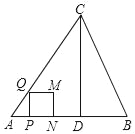
【题目】如图,在△ABC中,AB=AC=5,AB边上的高CD=4,点P从点A出发,沿AB以每秒3个单位长度的速度向终点B运动,当点P不与点A、B重合时,过点P作PQ⊥AB,交边AC或边BC于点Q,以PQ为边向右侧作正方形PQMN.设正方形PQMN与△ABC重叠部分图形的面积为S(平方单位),点P运动的时间为t(秒).
(1)直接写出tanB的值为 .
(2)求点M落在边BC上时t的值.
(3)当正方形PQMN与△ABC重叠部分为四边形时,求S与t之间的函数关系式.
(4)边BC将正方形PQMN的面积分为1:3两部分时,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市防洪大堤的横截面如图所示,已知AE∥BC,背水坡AB的坡度![]() ,且AB=26米.身高1.8米的小明竖直站立于A点,眼睛在M点处测得竖立的高压电线杆顶端D点的仰角为24°,已知地面CB宽30米,则高压电线杆CD的高度约为( )(结果精确到整数,参考数据:sin24°≈0.40,cos24°≈0.91,tan24°≈0.45)
,且AB=26米.身高1.8米的小明竖直站立于A点,眼睛在M点处测得竖立的高压电线杆顶端D点的仰角为24°,已知地面CB宽30米,则高压电线杆CD的高度约为( )(结果精确到整数,参考数据:sin24°≈0.40,cos24°≈0.91,tan24°≈0.45)

A. 33米 B. 34米 C. 35米 D. 36米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着网络的发展,我们的生活越来越方便,越来越多的人在网络上购物,微商这个行业也悄然兴起,很多人通过微信平台销售商品.
(1)某水果微商今年九月购进榴莲和奇异果共1000千克,它们的进价均为每千克24 元,然后以榴莲售价每千克45元,奇异果售价每千克36元的价格很快销售完,若该水果微商九月获利不低于17400元,求应购进榴莲至少多少千克?
(2)为了增加销售量,获得更大的利润,在进价不变的情况下,该水果微商十月决定调整售价,榴莲的售价在九月的基础上下调![]() (降价后的售价不低于进价),奇异果的售价在九月的基础上上涨
(降价后的售价不低于进价),奇异果的售价在九月的基础上上涨![]() ,同时,与(1)中获得的最低利润时的销售量相比,榴莲的销售量下降了
,同时,与(1)中获得的最低利润时的销售量相比,榴莲的销售量下降了![]() ,而奇异果的销售量上升了
,而奇异果的销售量上升了![]() ,结果十月的销售额比九月增加了600元.求
,结果十月的销售额比九月增加了600元.求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为鼓励大学毕业生自主创业,某市政府出台了相关政策:由政府协调,本市企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担.李明按照相关政策投资销售本市生产的一种新型节能灯.已知这种节能灯的成本价为每件10元,出厂价为每件12元,每月销售量y(件)与销售单价x(元)之间的关系近似满足一次函数:y=-10x+500.
(1)李明在开始创业的第一个月将销售单价定为20元,那么政府这个月为他承担的总差价为多少元?
(2)设李明获得的利润为W(元),当销售单价定为多少元时,每月可获得最大利润?
(3)物价部门规定,这种节能灯的销售单价不得高于25元.如果李明想要每月获得的利润不低于3000元,那么政府为他承担的总差价最少为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.
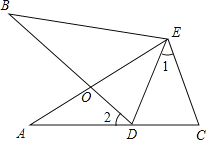
(1)求证:∠BDE=∠C;
(2)求证:△AEC≌△BED;
(3)若∠2=40°,则∠BDE=______°.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com