
【题目】如图,在△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,H是BC边的中点,连结DH、BE与相交于点G,以下结论中正确的结论有( ) (1.)△ABC是等腰三角形 (2.)BF=AC
(3.)BH:BD:BC=1: ![]() (4.)GE2+CE2=BG2 .
(4.)GE2+CE2=BG2 . 
A.1个
B.2个
C.3个
D.4个
【答案】C
【解析】解:(1.)∵BE平分∠ABC,∴∠ABE=∠CBE,
∵CD⊥AB,
∴∠ABE+∠A=90°,∠CBE+∠ACB=90°,
∴∠A=∠BCA,
∴AB=BC,
∴△ABC是等腰三角形;
故(1)正确;
(2.)∵CD⊥AB,BE⊥AC,
∴∠BDC=∠ADC=∠AEB=90°,
∴∠A+∠ABE=90°,∠ABE+∠DFB=90°,
∴∠A=∠DFB,
∵∠ABC=45°,∠BDC=90°,
∴∠DCB=90°﹣45°=45°=∠DBC,
∴BD=DC,
在△BDF和△CDA中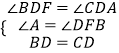 ,
,
∴△BDF≌△CDA(AAS),
∴BF=AC;
故(2)正确;
(3.)∵在△BCD中,∠CDB=90°,∠DBC=45°,
∴∠DCB=45°,
∴BD=CD,BC= ![]() BD.
BD.
由点H是BC的中点,
∴DH=BH=CH= ![]() BC,
BC,
∴BD= ![]() BH,
BH,
∴BH:BD:BC=BH: ![]() BH:2BH=1:
BH:2BH=1: ![]() :2.
:2.
故(3)错误;
(4.)由(2)知:BF=AC,
∵BF平分∠DBC,
∴∠ABE=∠CBE,
又∵BE⊥AC,
∴∠AEB=∠CEB,
在△ABE与△CBE中, ,
,
∴△ABE≌△CBE(AAS),
∴CE=AE= ![]() AC,
AC,
∴CE= ![]() AC=
AC= ![]() BF;
BF;
连接CG.
∵BD=CD,H是BC边的中点,
∴DH是BC的中垂线,
∴BG=CG,
在Rt△CGE中有:CG2=CE2+GE2 ,
∴CE2+GE2=BG2 .
故(4)正确.
综上所述,正确的结论由3个.
故选:C.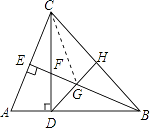
【考点精析】本题主要考查了勾股定理的概念的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能正确解答此题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】若关于x的方程(m﹣2)x2﹣2x+1=0有两个不等的实根,则m的取值范围是( )
A. m<3B. m≤3C. m<3且m≠2D. m≤3且m≠2
查看答案和解析>>
科目:初中数学 来源: 题型:
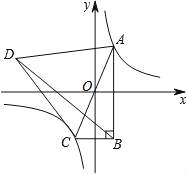
【题目】如图,已知双曲线y=![]() (k≠0)与正比例函数y=mx(m≠0)交于A、C两点,以AC为边作等边三角形ACD,且S△ACD=20
(k≠0)与正比例函数y=mx(m≠0)交于A、C两点,以AC为边作等边三角形ACD,且S△ACD=20![]() ,再以AC为斜边作直角三角形ABC,使AB∥y轴,连接BD.若△ABD的周长比△BCD的周长多4,则k的值是_______.
,再以AC为斜边作直角三角形ABC,使AB∥y轴,连接BD.若△ABD的周长比△BCD的周长多4,则k的值是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】鸡兔同笼是我国古代著名趣题之一.大约在1500年前,《孙子算经》中就记载了这个有趣的问题,书中是这样叙述的:“今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?”这四句话的意思是:有若干只鸡兔同在一个笼子里,从上面数,有35个头;从下面数有94只脚.问笼中各有几只鸡和兔?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列解方程组的方法,然后解决有关问题.
解方程组 ![]()
我们如果直接考虑消元,那么非常麻烦,而采用下列解法则轻而易举.
①﹣②,得2x+2y=2,即x+y=1 ③
③×16,得16x+16y=16 ④
②﹣④得x=﹣1,从而y=2
所以原方程组的解是 ![]()
(1)请你用上述方法解方程组 ![]()
(2)试猜测关于x、y的二元一次方程组 ![]() (a≠b)的解是什么?并加以验证.
(a≠b)的解是什么?并加以验证.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】第六次全国人口普查公布的数据表明,登记的全国人靠数量约为1 340 000 000人.这个数据用科学记数法表示为( )
A、134×107人B、13.4×108人
C、1.34×109人D、1.34×1010人
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com