
分析 如图1中,当DE⊥AB时,DE最小,即CD最小,根据已知条件得到△DEB是等腰直角三角形,设CD=DE=x,则DE=EB=x,∠DEB=90°,DB=$\sqrt{2}$x,解直角三角形得到结论,②如图2中,当E与A重合时,DE最大,即CD最大,作AH⊥CB于H,设CD=DE=x,在Rt△AHB中,易知AH=HB=4,∠AHB=90°,HD=x-2,DE=x,根据勾股定理即可得到结论.
解答 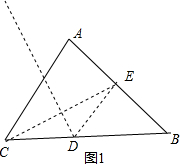 解:①如图1中,∵CD=DE,
解:①如图1中,∵CD=DE,
∴当DE⊥AB时,DE最小,即CD最小,
∵∠B=45°,
∴△DEB是等腰直角三角形,
设CD=DE=x,则DE=EB=x,∠DEB=90°,DB=$\sqrt{2}$x,
∵BC=6,
∴x+$\sqrt{2}$x=6,
∴x=6$\sqrt{2}$-6,
②如图2中,当E与A重合时,作AH⊥CB于H,设CD=DE=x,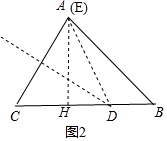
在Rt△AHB中,易知AH=HB=4,∠AHB=90°,HD=x-2,DE=x,
∴x2=42+(x-2)2,
∴x=5,
综上可知,CD的最大值为5,最小值为6$\sqrt{2}$-6,
∴CD的取值范围是6$\sqrt{2}$-6≤CD≤5,
故答案为6$\sqrt{2}$-6≤CD≤5.
点评 本题考查了折叠的性质,等腰直角三角形的判定和性质,等腰三角形的性质,正确的作出图形是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\frac{1}{2}$ | C. | 0 | D. | -2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 原料 维生素及价格 | A种原料 | B种原料 |
| 维生素C(单位/千克) | 600 | 100 |
| 原料价格(元/千克) | 6 | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
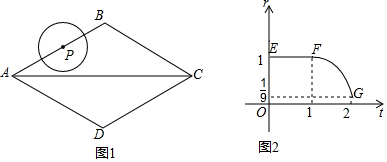
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①②③④ | B. | ①②③ | C. | ①③④ | D. | ②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
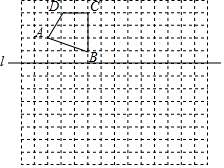 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点四边形ABCD(顶点是网格线的交点)和直线l,按要求画图.
如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点四边形ABCD(顶点是网格线的交点)和直线l,按要求画图.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 项目 品种 | A | B |
| 年亩产(单位:千克) | 1200 | 2000 |
| 采摘价格 (单位:元/千克) | 60 | 40 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com