
【题目】已知关于![]() 的一元二次方程
的一元二次方程![]() .
.
(1)求证:无论![]() 取何实数,方程总有两个不相等的实数根;
取何实数,方程总有两个不相等的实数根;
(2)若方程的一个根是3,求![]() 的值及方程的另一个根.
的值及方程的另一个根.
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:初中数学 来源: 题型:
【题目】如图,直角三角形的直角顶点在坐标原点,∠OAB=30°,若点A在反比例函数y=![]() (x>0)的图象上,则经过点B的反比例函数解析式为( )
(x>0)的图象上,则经过点B的反比例函数解析式为( )

A. y=﹣![]() B. y=﹣
B. y=﹣![]() C. y=﹣
C. y=﹣![]() D. y=
D. y=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
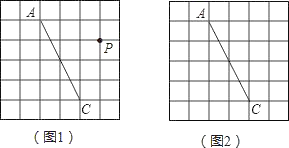
【题目】图1、图2是两张形状和大小完全相同的方格纸,方格纸中每个小正方形的边长均为1,线段AC的两个端点均在小正方形的顶点上.
(1)如图1,点P在小正方形的顶点上,在图1中作出点P关于直线AC的对称点Q,连接AQ、QC、CP、PA,并直接写出四边形AQCP的周长;
(2)在图2中画出一个以线段AC为对角线、面积为6的矩形ABCD,且点B和点D均在小正方形的顶点上.
查看答案和解析>>
科目:初中数学 来源: 题型:
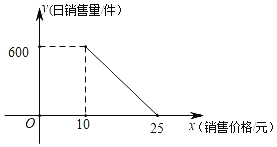
【题目】奏响复工复产“协奏曲”,防疫复产两不误.2020年2月5日,四川省出台《关于应对新型冠状病毒肺炎疫情缓解中小企业生产经营困难的政策措施》,推出减负降成本、破解融资难、财政补贴和税收减免、稳岗支持等13条举措,携手中小企业共渡难关.某企业积极复工复产,生产某种产品成本为9元/件,经过市场调查获悉,日销售量y(件)与销售价格x(元/件)的函数关系如图所示:
(1)求出y与x之间的函数表达式;
(2)当销售价格为多少元时,该企业日销售额为6000元?
(3)若该企业每销售1件产品可以获得2元财政补贴,则当销售价格x为何值时,该企业可以获最大日利润,最大日利润值为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
上课时孙老师提出这样一个问题:对于任意实数![]() ,关于
,关于![]() 的不等式
的不等式![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
小明的思路是:原不等式等价于![]() ,设函数
,设函数![]() ,
,![]() ,画出两个函数的图象的示意图,于是原问题转化为函数
,画出两个函数的图象的示意图,于是原问题转化为函数![]() 的图象在
的图象在![]() 的图象上方时
的图象上方时![]() 的取值范围.
的取值范围.

请结合小明的思路回答:
对于任意实数![]() ,关于
,关于![]() 的不等式
的不等式![]() 恒成立,则
恒成立,则![]() 的取值范围是_____.
的取值范围是_____.
参考小明思考问题的方法,解决问题:
关于![]() 的方程
的方程![]() 在
在![]() 范围内有两个解,求
范围内有两个解,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】光明中学在体育用品商店购进![]() 、
、![]() 两种型号的冰刀,购买
两种型号的冰刀,购买![]() 种型号冰刀花费2400元,购买
种型号冰刀花费2400元,购买![]() 种型号冰刀花费了l950元,且购买
种型号冰刀花费了l950元,且购买![]() 种型号冰刀数量是购买
种型号冰刀数量是购买![]() 种型号冰刀数量的2倍,已知购买一副
种型号冰刀数量的2倍,已知购买一副![]() 种型号冰刀比购买一副
种型号冰刀比购买一副![]() 种型号冰刀多花50元.
种型号冰刀多花50元.
(1)求购买一副![]() 种型号、一副
种型号、一副![]() 种型号的冰刀各需多少元?
种型号的冰刀各需多少元?
(2)该学校决定再次购进![]() 、
、![]() 两种型号冰刀共30副,恰逢百货商场对两种型号冰刀的售价进行调整,
两种型号冰刀共30副,恰逢百货商场对两种型号冰刀的售价进行调整,![]() 种型号冰刀售价比第一次购买时提高了
种型号冰刀售价比第一次购买时提高了![]() ,
,![]() 种型号冰刀按第一次购买时售价的9折出售,如果这所中学此次购买
种型号冰刀按第一次购买时售价的9折出售,如果这所中学此次购买![]() 、
、![]() 两种型号冰刀的总费用不超过3220元,那么该学校此次最多可购买多少副
两种型号冰刀的总费用不超过3220元,那么该学校此次最多可购买多少副![]() 种型号冰刀?
种型号冰刀?
查看答案和解析>>
科目:初中数学 来源: 题型:
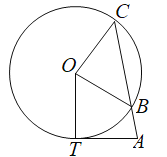
【题目】如图,已知AT切圆O于点T,点B在圆O上,且![]() ,连接AB并延长交圆O于点C,圆O的半径为2,若AT的长恰好为2.
,连接AB并延长交圆O于点C,圆O的半径为2,若AT的长恰好为2.
(1)求证:△BOC是等腰直角三角形;
(2)求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、F,连接BD交OF于点E.
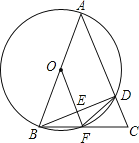
(1)求证:OF⊥BD;
(2)若AB=![]() ,DF=
,DF=![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com