
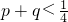 ;
; 时,y=x2+2px-q>0,即
时,y=x2+2px-q>0,即 -p-q>0,
-p-q>0,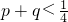 .
.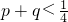 (p,q是实数),求证:方程x2+2px-q=0没有实数根.
(p,q是实数),求证:方程x2+2px-q=0没有实数根.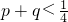 ,但原方程为x2=0有两个相等的实数根,所以(2)中的逆命题不正确.
,但原方程为x2=0有两个相等的实数根,所以(2)中的逆命题不正确. 时,y=x2+2px-q>0,即
时,y=x2+2px-q>0,即 -p-q>0,即可证明;
-p-q>0,即可证明;

 全能练考卷系列答案
全能练考卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com