

科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 中,∠F="90°,点B、C分别在AD、FD上,以AB为直径的半圆O" 过点C,
中,∠F="90°,点B、C分别在AD、FD上,以AB为直径的半圆O" 过点C, ,
, 且点E恰好落在直径AB上.
且点E恰好落在直径AB上. _____
_____ __;并证明你的结论.
__;并证明你的结论.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
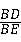 =
=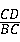 ;
;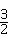 AB,求tan∠CDF的值.
AB,求tan∠CDF的值.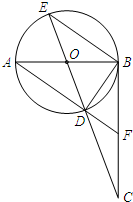
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 行速度.(精确到0.1海里/时,参考数据:
行速度.(精确到0.1海里/时,参考数据: ≈1.41,
≈1.41, ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
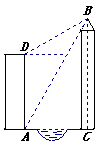
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 .容易知道一个角的大小与这个角的正对值也是相互
.容易知道一个角的大小与这个角的正对值也是相互 唯一确定的.根据上述角的正对定义,解下列问题:
唯一确定的.根据上述角的正对定义,解下列问题:
 ,试求sad A的值
,试求sad A的值
|
 | |||
 | |||
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com