
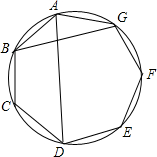
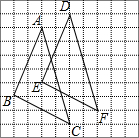
 已知边长为1的正七边形ABCDEFG中,对角线AD,BG的长分别为a,b(a≠b),求证:(a+b)2(a-b)=ab2.
已知边长为1的正七边形ABCDEFG中,对角线AD,BG的长分别为a,b(a≠b),求证:(a+b)2(a-b)=ab2. 分析 连结BD、EG、BE、DG,则BD=EG=GB=b,DG=BE=DA=a,DE=AB=AG=1,在四边形ABDG中,利用托勒密协定理可得ab=a+b,同理在四边形BDEG中,可得b=a2-b2=(a+b)(a-b),可得结论.
解答 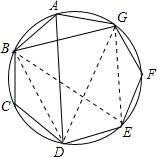 证明:连结BD、EG、BE、DG,则BD=EG=GB=b,DG=BE=DA=a,DE=AB=AG=1,在四边形ABDG中,由托勒密协定理,得AD•BG=AB•DG+BD•AG,
证明:连结BD、EG、BE、DG,则BD=EG=GB=b,DG=BE=DA=a,DE=AB=AG=1,在四边形ABDG中,由托勒密协定理,得AD•BG=AB•DG+BD•AG,
即ab=a+b ①,
同理在四边形BDEG中,得BE•DG=DE•BG+BD•GE,
即a2=b+b2,
∴b=a2-b2=(a+b)(a-b) ②,
①×②,得ab2=(a+b)2(a-b).
点评 本题主要考查了正多边形和圆,利用“在四边形中,两对角线的乘积是两组对边乘积的和”是解答此题的关键.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
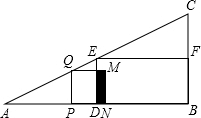 在△ABC中,∠B=90°,AB=12cm,BC=6cm,D、E、F分别为AB、AC边上的中点,若P为AB边上的一个动点,PQ⊥AB,交AC于Q,以PQ为一边,在点A的异侧作正方形PQMN,记正方形PQMN与矩形EDBF的公共部分的面积为y.
在△ABC中,∠B=90°,AB=12cm,BC=6cm,D、E、F分别为AB、AC边上的中点,若P为AB边上的一个动点,PQ⊥AB,交AC于Q,以PQ为一边,在点A的异侧作正方形PQMN,记正方形PQMN与矩形EDBF的公共部分的面积为y.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
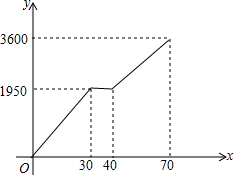 小颖和小亮上山游玩,小颖乘坐缆车,小亮步行,两人相约在山顶的缆车终点会合.已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍,小颖在小亮出发后40分钟后才乘上缆车,缆车的平均速度为180米/分.设小亮出发x分后行走的路程为y米.图中的折线表示小亮在整个行走过程中y随x的变化关系.
小颖和小亮上山游玩,小颖乘坐缆车,小亮步行,两人相约在山顶的缆车终点会合.已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍,小颖在小亮出发后40分钟后才乘上缆车,缆车的平均速度为180米/分.设小亮出发x分后行走的路程为y米.图中的折线表示小亮在整个行走过程中y随x的变化关系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,每个小正方形的边长为1,三角形ABC的三个顶点都在格点(小正方形的顶点)上,
如图,每个小正方形的边长为1,三角形ABC的三个顶点都在格点(小正方形的顶点)上,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com