
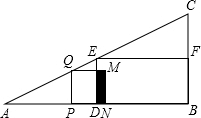
 在△ABC中,∠B=90°,AB=12cm,BC=6cm,D、E、F分别为AB、AC边上的中点,若P为AB边上的一个动点,PQ⊥AB,交AC于Q,以PQ为一边,在点A的异侧作正方形PQMN,记正方形PQMN与矩形EDBF的公共部分的面积为y.
在△ABC中,∠B=90°,AB=12cm,BC=6cm,D、E、F分别为AB、AC边上的中点,若P为AB边上的一个动点,PQ⊥AB,交AC于Q,以PQ为一边,在点A的异侧作正方形PQMN,记正方形PQMN与矩形EDBF的公共部分的面积为y.分析 (1)先根据AP的长,求出PQ的值,然后看看正方形与矩形是否重合,若重合求出重合部分的线段的长,然后根据矩形的面积计算公式进行求解即可.
(2)要分四种情况进行讨论:
①当N在D点或D点左侧时,当正方形PQMN的边MN与矩形EDBF的边ED重合时,利用相似三角形的性质可得出x=3,即0<x≤3时,此时正方形与矩形没有重合,因此y=0;
②当N在D点右侧,而P点在D点左侧或与D点重合时,即4<x≤6,此时正方形与矩形重合的面积应该是以DN为长,NM为宽的矩形,DN=PN-PD=PN-(AD-AP)=x-(6-$\frac{1}{2}$x)=$\frac{3}{2}$x-6.而NM=PQ=$\frac{1}{2}$x,因此重合部分的面积应该是y=($\frac{3}{2}$x-6)×$\frac{1}{2}$x=$\frac{3}{4}$x2-3x;
③当P在D点右侧,而N点在B点左侧或与B点重合时,即6<x≤8时,此时正方形重合部分的面积应该是以正方形边长为长,DE为宽的矩形的面积,PN=$\frac{1}{2}$x,DE=3,因此此时重合部分的面积是y=$\frac{1}{2}$x×3=$\frac{3}{2}$x;
④当P在B左侧时,而N点在AB延长线上时,即8<x<12时,此时重合部分的面积应该是以DE长为宽,PA长为长的矩形的面积.BP=AB-AP=12-x,BF=DE=3,因此此时重合部分的面积应该是y=(12-x)×3=36-3x.
(3)将y=3代入(2)的式子中,看看求出的x哪个符合条件即可.
解答 解:(1)∵在Rt△ABC中,∠B=90°,BC=6cm,AB=12cm,
∴tanA=$\frac{BC}{AB}$=$\frac{1}{2}$,
∵D是AB中点,
∴DE是△ABC的中位线,
∴AD=BD=6cm,DE=3cm,
∴Rt△APQ中,AP=5cm,
∴PQ=AP•tanA=5×$\frac{1}{2}$=2.5cm,
∴DN=AN-AD=AP+PN-AD=5+2.5-6=1.5,
∴重合部分的面积应该是y=DN×MN=2.5×1.5=3.75cm2;
(2)设AP=xcm,则: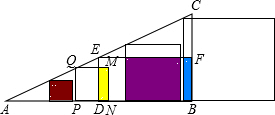 ①当N在D点或D点左侧时,当正方形PQMN的边MN与矩形EDBF的边ED重合时,利用相似三角形的性质可得出x=3,即0<x≤2时,此时正方形与矩形没有重合,因此y=0;
①当N在D点或D点左侧时,当正方形PQMN的边MN与矩形EDBF的边ED重合时,利用相似三角形的性质可得出x=3,即0<x≤2时,此时正方形与矩形没有重合,因此y=0;
②当N在D点右侧,而P点在D点左侧或与D点重合时,即4<x≤6,此时正方形与矩形重合的面积应该是以DN为长,NM为宽的矩形,DN=PN-PD=PN-(AD-AP)=x-(6-$\frac{1}{2}$x)=$\frac{3}{2}$x-6.而NM=PQ=$\frac{1}{2}$x,因此重合部分的面积应该是y=($\frac{3}{2}$x-6)×$\frac{1}{2}$x=$\frac{3}{4}$x2-3x;
③当P在D点右侧,而N点在B点左侧或与B点重合时,即6<x≤8时,此时正方形重合部分的面积应该是以正方形边长为长,DE为宽的矩形的面积,PN=$\frac{1}{2}$x,DE=3,因此此时重合部分的面积是y=$\frac{1}{2}$x×3=$\frac{3}{2}$x;
④当P在B左侧时,而N点在AB延长线上时,即8<x<12时,此时重合部分的面积应该是以DE长为宽,PA长为长的矩形的面积.BP=AB-AP=12-x,BF=DE=3,因此此时重合部分的面积应该是y=(12-x)×3=36-3x;
(3)当0<x≤4,y=3,即$\frac{3}{4}$x2-3x=3,解得:x=2+2$\sqrt{2}$,(负值舍去),
当6<x≤8,y=3,即3=$\frac{3}{2}$x,解得:x=2,(不合题意舍去)
当8<x<12,y=3,即36-3x=3,解得x=11.
∴当x=2+2$\sqrt{2}$,或行11时,y=3.
点评 本题主要考查了直角三角形的性质,正方形的性质,中位线定理以及解直角三角形的应用等知识点,要注意(2)(3)中,正方形的位置不同时,函数解析式是不同的,要分类讨论,不要漏解.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
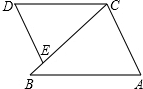 如图,AB∥CD,点E在BC上,且CD=CE,则∠B的取值范围是( )
如图,AB∥CD,点E在BC上,且CD=CE,则∠B的取值范围是( )| A. | 0°~90° | B. | 0°~180° | C. | 0°~60° | D. | 90°~180° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com