练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    20．以下结论正确的是（　　）
    A．对角线相等，且一组对角相等的四边形是平行四边形
    B．一对邻角的和为180°的四边形是平行四边形
    C．一组对边平行且相等的四边形是平行四边形
    D．两条对角线相互垂直的四边形是平行四边形

    分析 分别利用平行四边形的判定方法结合梯形的判定方法分析得出答案．

    解答 解：A、对角线相等，且一组对角相等的四边形无法确定是平行四边形，故此选项不合题意；
    B、一对邻角的和为180°的四边形是平行四边形，错误，有可能是梯形，故此选项不合题意；
    C、一组对边平行且相等的四边形是平行四边形，正确，符合题意；
    D、两条对角线相互垂直的四边形无法确定是平行四边形，故此选项不合题意；
    故选：C．

    点评 此题主要考查了平行四边形的判定，正确把握相关判定方法是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

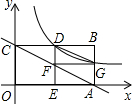    10．如图，已知矩形OABC中，点A（2，0）、C（0，1）．点D是边BC的中点，过点D作DE⊥OA于点E，双曲线y=$\frac{k}{x}$过点D交AB于点G，直线AC交DE于点F，连接DG、FG．
    （1）求点D的坐标；
    （2）求k的值与直线AC的解析式；
    （3）求四边形DCFG的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    11．用计算器比较大小：$\sqrt{6}$＜$\root{3}{15}$．（填“＞”、“＜”或“=”）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

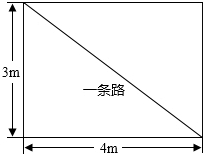    8．在“寻找滨河最美，拒绝不文明行为”系列活动中，细心的董明同学发现：学校六号楼前有一块长方形花圃（如图所示），有极少数人为了避开拐角走“捷径”，在花圃内走出了一条“路”，请你计算，他们仅仅少走了4步路（假设2步为1米），却踩伤了花草．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

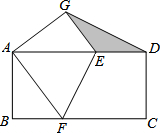    15．如图，矩形纸片ABCD中，AB=4，BC=8，将纸片折叠，使点C与点A重合，折痕为EF，点D的对应点为G，连接DG，则图中阴影部分面积是（　　）
    A．5B．3C．$\frac{36}{5}$D．$\frac{18}{5}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．（1）如图1，已知E是矩形ABCD的边AB上一点，EF⊥DE交BC于点F，证明：△ADE∽△BEF．
    这个相似的基本图形像字母K，可以称为“K”型相似，但更因为图形的结构特征是一条线上有3个垂直关系，也常被称为“一线三垂直”，那普通的3个等角又会怎样呢？
    （2）变式一如图2，已知等边三角形ABC，点D、E分别为BC，AC上的点，∠ADE=60°．
    ①图中有相似三角形吗？请说明理由．
    ②如图3，若将∠ADE在△ABC的内部（∠ADE两边不与BC重合），绕点D逆时针旋转一定的角度，还有相似三角形吗？△BDF∽△CED（若有请写出相似三角形，没有则填“无”）
    （3）变式二如图4，隐藏变式1图形中的线段AE，在得到的新图形中．
    ①如果∠B=∠C=∠ADE=50°，图中有相似三角形吗？请说明理由．
    ②如图5，若∠B=∠C=∠ADE=∠a，∠a为任意角，还有相似三角形吗？△ABD∽△DCE．（若有请写出相似三角形，没有则填“无”）
    （4）变式三，已知，相邻两条平行直线间的距离相等，若等腰直角△ABC的三个顶点分别在这三条平行直线上，则cosa的值是$\frac{3\sqrt{10}}{10}$（直接写出结果）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．已知函数y=x+k+1是正比例函数，则k的值为（　　）
    A．1B．-1C．0D．±1

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．（1）【问题发现】
    如图1，在Rt△ABC中，AB=AC=2，∠BAC=90°，点D为BC的中点，以CD为一边作正方形CDEF，点E恰好与点A重合，则线段BE与AF的数量关系为BE=$\sqrt{2}$AF
    （2）【拓展研究】
    在（1）的条件下，如果正方形CDEF绕点C旋转，连接BE，CE，AF，线段BE与AF的数量关系有无变化？请仅就图2的情形给出证明；
    （3）【问题发现】
    当正方形CDEF旋转到B，E，F三点共线时候，直接写出线段AF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．小明饶着一个五边形的花圃走了一圈，他一共转了多少度（　　）
    A．180°B．360°C．540°D．720°

    查看答案和解析>>

    同步练习册答案