
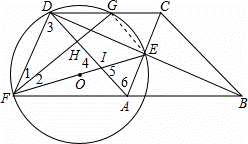
如图,四边形ABCD为菱形,对角线AC,BD相交于点E,F是边BA延长线上一点,连接EF,以EF为直径作⊙O,交DC于D,G两点,AD分别于EF,GF交于I,H两点.
(1)求∠FDE的度数;
(2)试判断四边形FACD的形状,并证明你的结论;
(3)当G为线段DC的中点时,
①求证:FD=FI;
②设AC=2m,BD=2n,求⊙O的面积与菱形ABCD的面积之比.
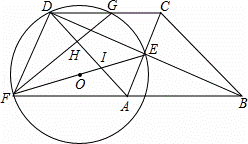
解:(1)∵EF是⊙O的直径,∴∠FDE=90°;
(2)四边形FACD是平行四边形.
理由如下:
∵四边形ABCD是菱形,
∴AB∥CD,AC⊥BD,
∴∠AEB=90°.
又∵∠FDE=90°,
∴∠AEB=∠FDE,
∴AC∥DF,
∴四边形FACD是平行四边形;
(3)①连接GE,如图.
∵四边形ABCD是菱形,∴点E为AC中点.
∵G为线段DC的中点,∴GE∥DA,
∴∠FHI=∠FGE.
∵EF是⊙O的直径,∴∠FGE=90°,
∴∠FHI=90°.
∵∠DEC=∠AEB=90°,G为线段DC的中点,
∴DG=GE,
∴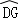 =
=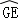 ,
,
∴∠1=∠2.
∵∠1+∠3=90°,∠2+∠4=90°,
∴∠3=∠4,
∴FD=FI;
②∵AC∥DF,∴∠3=∠6.
∵∠4=∠5,∠3=∠4,
∴∠5=∠6,∴EI=EA.
∵四边形ABCD是菱形,四边形FACD是平行四边形,
∴DE=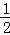 BD=n,AE=
BD=n,AE=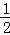 AC=m,FD=AC=2m,
AC=m,FD=AC=2m,
∴EF=FI+IE=FD+AE=3m.
在Rt△EDF中,根据勾股定理可得:
n2+(2m)2=(3m)2,
即n= m,
m,
∴S⊙O=π( )2=
)2= πm2,S菱形ABCD=
πm2,S菱形ABCD=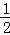 •2m•2n=2mn=2
•2m•2n=2mn=2 m2,
m2,
∴S⊙O:S菱形ABCD=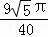 .
.


科目:初中数学 来源: 题型:
用配方法解一元二次方程x2﹣6x﹣4=0,下列变形正确的是( )
|
| A. | (x﹣6)2=﹣4+36 | B. | (x﹣6)2=4+36 | C. | (x﹣3)2=﹣4+9 | D. | (x﹣3)2=4+9 |
查看答案和解析>>
科目:初中数学 来源: 题型:
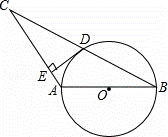
如图,⊙O的直径AB=4,∠ABC=30°,BC交⊙O于D,D是BC的中点.
(1)求BC的长;
(2)过点D作DE⊥AC,垂足为E,求证:直线DE是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
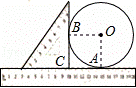
如图,圆形铁片与直角三角尺、直尺紧靠在一起平放在桌面上.已知铁片的圆心为O,三角尺的直角顶点C落在直尺的10cm处,铁片与直尺的唯一公共点A落在直尺的14cm处,铁片与三角尺的唯一公共点为B,下列说法错误的是( )
|
| A. | 圆形铁片的半径是4cm | B. | 四边形AOBC为正方形 |
|
| C. | 弧AB的长度为4πcm | D. | 扇形OAB的面积是4πcm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
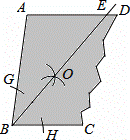
如图,一块余料ABCD,AD∥BC,现进行如下操作:以点B为圆心,适当长为半径画弧,分别交BA,BC于点G,H;再分别以点G,H为圆心,大于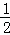 GH的长为半径画弧,两弧在∠ABC内部相交于点O,画射线BO,交AD于点E.
GH的长为半径画弧,两弧在∠ABC内部相交于点O,画射线BO,交AD于点E.
(1)求证:AB=AE;
(2)若∠A=100°,求∠EBC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
永州市双牌县的阳明山风光秀丽,历史文化源远流长,尤以山顶数万亩野生杜鹃花最为壮观,被誉为“天下第一杜鹃红”.今年“五一”期间举办了“阳明山杜鹃花旅游文化节”,吸引了众多游客前去观光赏花.在文化节开幕式当天,从早晨8:00开始每小时进入阳明山景区的游客人数约为1000人,同时每小时走出景区的游客人数约为600人,已知阳明上景区游客的饱和人数约为2000人,则据此可知开幕式当天该景区游客人数饱和的时间约为( )
|
| A. | 10:00 | B. | 12:00 | C. | 13:00 | D. | 16:00 |
查看答案和解析>>
科目:初中数学 来源: 题型:
国家森林城市的创建极大地促进了森林资源的增长,美化了城市环境,提升了市民的生活质量,截至2014年.全国已有21个省、自治区、直辖市的75个城市获得了“国家森林城市”乘号.永州市也在积极创建“国家森林城市”.据统计近两年全市投入“创森”资金约为365000000元,365000000用科学记数法表示为
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com