练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，一块余料ABCD，AD∥BC，现进行如下操作：以点B为圆心，适当长为半径画弧，分别交BA，BC于点G，H；再分别以点G，H为圆心，大于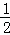GH的长为半径画弧，两弧在∠ABC内部相交于点O，画射线BO，交AD于点E．

    （1）求证：AB=AE；

    （2）若∠A=100°，求∠EBC的度数．

     


    （1）证明：∵AD∥BC，

    ∴∠AEB=∠EBC．

    由BE是∠ABC的角平分线，

    ∴∠EBC=∠ABE，

    ∴∠AEB=∠ABE，

    ∴AB=AE；

    （2）由∠A=100°，∠ABE=∠AEB，得

    ∠ABE=∠AEB=40°．

    由AD∥BC，得

    ∠EBC=∠AEB=40°．

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    在“绿满鄂南”行动中，某社区计划对面积为1800m2的区域进行绿化．经投标，由甲、乙两个工程队来完成，已知甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍，并且在独立完成面积为400m2区域的绿化时，甲队比乙队少用4天．

    （1）求甲、乙两工程队每天能完成绿化的面积．

    （2）设甲工程队施工x天，乙工程队施工y天，刚好完成绿化任务，求y与x的函数解析式．

    （3）若甲队每天绿化费用是0.6万元，乙队每天绿化费用为0.25万元，且甲乙两队施工的总天数不超过26天，则如何安排甲乙两队施工的天数，使施工总费用最低？并求出最低费用．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，圆O的直径AB=8，AC=3CB，过C作AB的垂线交圆O于M，N两点，连结MB，则∠MBA的余弦值为　　．

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    下列式子没有意义的是（　　）

    　

    A．

    B．

    C．

    D．

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    两组邻边分别相等的四边形叫做“筝形”，如图，四边形ABCD是一个筝形，其中AD=CD，AB=CB，詹姆斯在探究筝形的性质时，得到如下结论：

    ①AC⊥BD；②AO=CO=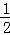AC；③△ABD≌△CBD，

    其中正确的结论有（　　）

    　

    A．

    0个

    B．

    1个

    C．

    2个

    D．

    3个

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


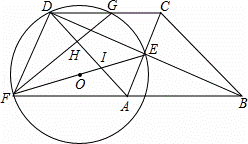
    如图，四边形ABCD为菱形，对角线AC，BD相交于点E，F是边BA延长线上一点，连接EF，以EF为直径作⊙O，交DC于D，G两点，AD分别于EF，GF交于I，H两点．

    （1）求∠FDE的度数；

    （2）试判断四边形FACD的形状，并证明你的结论；

    （3）当G为线段DC的中点时，

    ①求证：FD=FI；

    ②设AC=2m，BD=2n，求⊙O的面积与菱形ABCD的面积之比．

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，P是⊙O外一点，PA、PB分别交⊙O于C、D两点，已知和所对的圆心角分别为90°和50°，则∠P=（　　）

    　

    A．

    45°

    B．

    40°

    C．

    25°

    D．

    20°

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在四边形ABCD中，∠A=∠BCD=90°，BC=DC．延长AD到E点，使DE=AB．

    （1）求证：∠ABC=∠EDC；

    （2）求证：△ABC≌△EDC．

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    正八边形一个内角的度数为　

    查看答案和解析>>

    同步练习册答案