
在“绿满鄂南”行动中,某社区计划对面积为1800m2的区域进行绿化.经投标,由甲、乙两个工程队来完成,已知甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍,并且在独立完成面积为400m2区域的绿化时,甲队比乙队少用4天.
(1)求甲、乙两工程队每天能完成绿化的面积.
(2)设甲工程队施工x天,乙工程队施工y天,刚好完成绿化任务,求y与x的函数解析式.
(3)若甲队每天绿化费用是0.6万元,乙队每天绿化费用为0.25万元,且甲乙两队施工的总天数不超过26天,则如何安排甲乙两队施工的天数,使施工总费用最低?并求出最低费用.
解:(1)设乙工程队每天能完成绿化的面积是xm2,
根据题意得: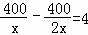 ,
,
解得:x=50,
经检验,x=50是原方程的解,
则甲工程队每天能完成绿化的面积是50×2=100(m2),
答:甲、乙两工程队每天能完成绿化的面积分别是100m2、50m2;
(2)根据题意,得:100x+50y=1800,
整理得:y=36﹣2x,
∴y与x的函数解析式为:y=36﹣2x.
(3)∵甲乙两队施工的总天数不超过26天,
∴x+y≤26,
∴x+36﹣2x≤26,
解得:x≥10,
设施工总费用为w元,根据题意得:
w=0.6x+0.25y=0.6x+0.25×(36﹣2x)=0.1x+9,
∵k=0.1>0,
∴w随x减小而减小,
∴当x=10时,w有最小值,最小值为0.1×10+9=10,
此时y=36﹣20=16.
答:安排甲队施工10天,乙队施工16天时,施工总费用最低


科目:初中数学 来源:2014-2015学年江苏省滨海县八年级上学期期末考试数学试卷(解析版) 题型:解答题
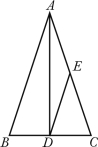
(本题满分8分)如图,等腰△ABC中,AB=AC, BC=10,角平分线AD=12,点E是AC中点,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
.雾霾天气严重影响市民的生活质量.在今年寒假期间,某校八年一班的综合实践小组同学对“雾霾天气的主要成因”随机调查了所在城市部分市民,并对调查结果进行了整理,绘制了如下不完整的统计图表,观察分析并回答下列问题.
⑴本次被调查的市民共有多少人?
⑵分别补全条形统计图和扇形统计图, 并计算图2中区域B所对应的扇形圆心角的度数.
⑶若该市有100万人口,请估计持有
A、B两组主要成因的市民有多少人?

| 组别 | 雾霾天气的主要成因 | 百分比 |
| A | 工业污染 | 45% |
| B | 汽车尾气排放 |
|
| C | 炉烟气排放 | 15% |
| D | 其他(滥砍滥伐等) |
|
查看答案和解析>>
科目:初中数学 来源: 题型:
用配方法解一元二次方程x2﹣6x﹣4=0,下列变形正确的是( )
|
| A. | (x﹣6)2=﹣4+36 | B. | (x﹣6)2=4+36 | C. | (x﹣3)2=﹣4+9 | D. | (x﹣3)2=4+9 |
查看答案和解析>>
科目:初中数学 来源: 题型:
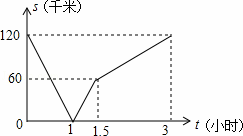
甲骑摩托车从A地去B地,乙开汽车从B地去A地,同时出发,匀速行驶,各自到达终点后停止,设甲、乙两人间距离为s(单位:千米),甲行驶的时间为t(单位:小时),s与t之间的函数关系如图所示,有下列结论:
①出发1小时时,甲、乙在途中相遇;
②出发1.5小时时,乙比甲多行驶了60千米;
③出发3小时时,甲、乙同时到达终点;
④甲的速度是乙速度的一半.
其中,正确结论的个数是( )
|
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:
国家统计局数据显示,截至2014年末全国商品房待售面积约为62200万平方米,该数据用科学记数法可表示为( )
|
| A. | 6.22×104 | B. | 6.22×107 | C. | 6.22×108 | D. | 6.22×109 |
查看答案和解析>>
科目:初中数学 来源: 题型:
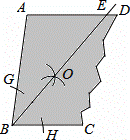
如图,一块余料ABCD,AD∥BC,现进行如下操作:以点B为圆心,适当长为半径画弧,分别交BA,BC于点G,H;再分别以点G,H为圆心,大于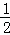 GH的长为半径画弧,两弧在∠ABC内部相交于点O,画射线BO,交AD于点E.
GH的长为半径画弧,两弧在∠ABC内部相交于点O,画射线BO,交AD于点E.
(1)求证:AB=AE;
(2)若∠A=100°,求∠EBC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com