
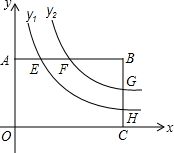
 如图,矩形OABC的两个顶点A,C分别在y轴和x轴上,边AB和BC与反比例函数y1=$\frac{4}{x}$(x>0)和y2=$\frac{k}{x}$(k>0,x>0)图象交于E,F和点H,G.AE:AF=2:3.
如图,矩形OABC的两个顶点A,C分别在y轴和x轴上,边AB和BC与反比例函数y1=$\frac{4}{x}$(x>0)和y2=$\frac{k}{x}$(k>0,x>0)图象交于E,F和点H,G.AE:AF=2:3.分析 (1)设E(a,b),根据已知条件求得F($\frac{3}{2}$a,b),分别代入解析式得出ab=4,$\frac{3}{2}$a•b=k,从而求得k=6,D得出反比例函数y2的解析式;
(2)把x=8分别代入y1=$\frac{4}{x}$和y2=$\frac{6}{x}$,即可求得CG、CH的值,然后根据GH=CG-CH即可求得.
解答 解:(1)设E(a,b),
∴AE=a,
∵AE:AF=2:3.
∴AF=$\frac{3}{2}$a,
∴F($\frac{3}{2}$a,b),
∵E是反比例函数y1=$\frac{4}{x}$(x>0)上的点,
∴ab=4,
∵F是反比例函数$\frac{k}{x}$(k>0,x>0)图象上的点,
∴$\frac{3}{2}$a•b=k,
∴k=$\frac{3}{2}$×4=6,
∴反比例函数y2的解析式为y2=$\frac{6}{x}$.
(2)把x=8分别代入y1=$\frac{4}{x}$和y2=$\frac{6}{x}$得,y1=$\frac{1}{2}$和y2=$\frac{3}{4}$,
∴CH=$\frac{1}{2}$,CG=$\frac{3}{4}$,
∴GH=CG-CH=$\frac{1}{4}$.
点评 本题考查了待定系数法求反比例函数的解析式以及反比例函数图象上点的坐标特征,利用形数结合解决此类问题,是非常有效的方法.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
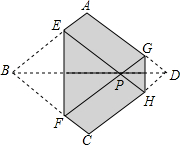 如图,菱形纸片ABCD的边长为2,折叠菱形纸片,将B、D两点重合在对角线BD上的同一点P处,折痕分别为EF、GH.重合点P在对角线BD上移动,设折痕EF的长为m.请你分别判断以下结论的真假,并给出理由.
如图,菱形纸片ABCD的边长为2,折叠菱形纸片,将B、D两点重合在对角线BD上的同一点P处,折痕分别为EF、GH.重合点P在对角线BD上移动,设折痕EF的长为m.请你分别判断以下结论的真假,并给出理由.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
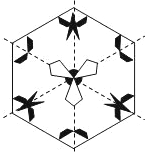 学习了旋转对称图形,小明与小东研究如图所示的图案.小明说:“只需要把该图案的$\frac{1}{6}$绕其中心分别旋转60°、120°、180°、240°、300°后,由前后的图形就可以共同组成该图案.”小东说:“错了,应该把该图案的把该图案的$\frac{1}{3}$绕其中心分别旋转120°、240°后,由前后的图形就可以共同组成该图案.”“你说的真对,我是一叶障目,不识泰山啊”.你觉得小东该说什么,请在横线上把小东的补充完整.
学习了旋转对称图形,小明与小东研究如图所示的图案.小明说:“只需要把该图案的$\frac{1}{6}$绕其中心分别旋转60°、120°、180°、240°、300°后,由前后的图形就可以共同组成该图案.”小东说:“错了,应该把该图案的把该图案的$\frac{1}{3}$绕其中心分别旋转120°、240°后,由前后的图形就可以共同组成该图案.”“你说的真对,我是一叶障目,不识泰山啊”.你觉得小东该说什么,请在横线上把小东的补充完整.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 为了探究代数式$\sqrt{{x^2}+4}+\sqrt{{{({9-x})}^2}+1}$的最小值,小明巧妙的运用了“数形结合”思想.具体方法是这样的:如图,C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC.已知AB=2,DE=1,BD=9,设BC=x.则$AC=\sqrt{{x^2}+4}$,$CE=\sqrt{{{({9-x})}^2}+1}$,则问题即转化成求AC+CE的最小值.
为了探究代数式$\sqrt{{x^2}+4}+\sqrt{{{({9-x})}^2}+1}$的最小值,小明巧妙的运用了“数形结合”思想.具体方法是这样的:如图,C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC.已知AB=2,DE=1,BD=9,设BC=x.则$AC=\sqrt{{x^2}+4}$,$CE=\sqrt{{{({9-x})}^2}+1}$,则问题即转化成求AC+CE的最小值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 每月水用量 | 单价 |
| 不超出6m3额额部分 | 2元/m3 |
| 超出6m3不超出10m3的部分 | 4元/m3 |
| 超出10m3的部分 | 8元/m3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com