
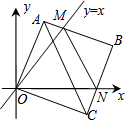
 在平面直角坐标系中,边长为3的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上,点O在原点.现将正方形OABC绕O点顺时针旋转,当A点第一次落在直线y=x上时停止旋转,旋转过程中,AB边交直线y=x于点M,BC边交x轴于点N(如图).在旋转正方形OABC的过程中,△MBN的周长为6.
在平面直角坐标系中,边长为3的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上,点O在原点.现将正方形OABC绕O点顺时针旋转,当A点第一次落在直线y=x上时停止旋转,旋转过程中,AB边交直线y=x于点M,BC边交x轴于点N(如图).在旋转正方形OABC的过程中,△MBN的周长为6. 分析 通过证△OAE≌△OCN(ASA)和△OME≌△OMN(SAS),把△MBN的各边整理成与正方形的边长有关的式子即可.
解答 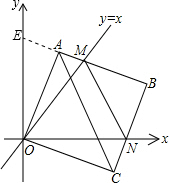 解:∵A点第一次落在直线y=x上时停止旋转,直线y=x与y轴的夹角是45°,
解:∵A点第一次落在直线y=x上时停止旋转,直线y=x与y轴的夹角是45°,
∴OA旋转了45°.
如图所示:延长BA交y轴于E点,
则∠AOE=45°-∠AOM,∠CON=90°-45°-∠AOM=45°-∠AOM,
∴∠AOE=∠CON.
又∵OA=OC,∠OAE=180°-90°=90°=∠OCN,
在△OAE和△OCN中,
$\left\{\begin{array}{l}{∠EOA=∠CON}\\{OA=OC}\\{∠OAE=∠OCN}\end{array}\right.$,
∴△OAE≌△OCN(ASA).
∴OE=ON,AE=CN.
在△OME和△OMN中,
$\left\{\begin{array}{l}{OE=ON}\\{∠EOM=∠MON}\\{OM=ON}\end{array}\right.$,
∴△OME≌△OMN(SAS).
∴MN=ME=AM+AE.
∴MN=AM+CN,
∴△MBN的周长为:MN+BN+BM=AM+CN+BN+BM=AB+BC=6.
故答案是:6.
点评 此题主要考查了旋转的性质以及全等三角形的判定与性质等知识,注意求一些线段的长度或角的度数,总要整理到已知线段的长度上或已知角的度数上进而得出是解题关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
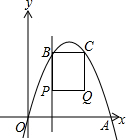 如图,在平面直角坐标系中,经过原点的抛物线y=-x2+4mx(m>0)与x轴的另一个交点为点A,过点P(1,m)作直线PB⊥x轴,交抛物线于点B,作点B关于抛物线对称轴的对称点C(点B、C不重合),连结BC,当点P、B不重合时,以BP、BC为边作矩形PBCQ,设矩形PBCQ的周长为l.
如图,在平面直角坐标系中,经过原点的抛物线y=-x2+4mx(m>0)与x轴的另一个交点为点A,过点P(1,m)作直线PB⊥x轴,交抛物线于点B,作点B关于抛物线对称轴的对称点C(点B、C不重合),连结BC,当点P、B不重合时,以BP、BC为边作矩形PBCQ,设矩形PBCQ的周长为l.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,BD是△ABC的角平分线,点E、F分别在边BC、AB上,且DE∥AB,∠DEF=∠A.
如图,BD是△ABC的角平分线,点E、F分别在边BC、AB上,且DE∥AB,∠DEF=∠A.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
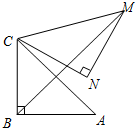 如图,Rt△ABC中,∠ABC=90°,AB=BC=2,将△ABC绕点C逆时针旋转60°,得到△MNC,连接BM,那么BM的长是$\sqrt{6}+\sqrt{2}$.
如图,Rt△ABC中,∠ABC=90°,AB=BC=2,将△ABC绕点C逆时针旋转60°,得到△MNC,连接BM,那么BM的长是$\sqrt{6}+\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,∠CAB=90°,AB=6,AC=4,CD是△ABC的中线,将△ABC沿直线CD翻折,点B′是点B的对应点,点E是线段CD上的点,如果∠CAE=∠BAB′,那么CE的长是$\frac{16}{5}$.
如图,在△ABC中,∠CAB=90°,AB=6,AC=4,CD是△ABC的中线,将△ABC沿直线CD翻折,点B′是点B的对应点,点E是线段CD上的点,如果∠CAE=∠BAB′,那么CE的长是$\frac{16}{5}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com