
 如图,BD是△ABC的角平分线,点E、F分别在边BC、AB上,且DE∥AB,∠DEF=∠A.
如图,BD是△ABC的角平分线,点E、F分别在边BC、AB上,且DE∥AB,∠DEF=∠A.分析 (1)先证明四边形ADEF为平行四边形得到AF=DE,再证明∠DBE=∠BDE得到BE=DE,则BE=AF;
(2)如图,根据平行线分线段成比例定理,由EF∥AC得到AF:AB=DM:BD,等线段代换得DE:AB=DM:BD,再由DE∥AB得到DE:AB=DN:BN,则DM:BD=DN:BN,然后利用比例的性质即可得到结论.
解答 证明:(1)∵DE∥AB,
∴∠A+∠ADE=180°,
∵∠DEF=∠A,
∴∠DEF+∠ADE=180°,
∴EF∥AD,
∴四边形ADEF为平行四边形,
∴AF=DE,
∵BD是△ABC的角平分线,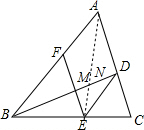
∴∠DBE=∠ABD,
∵DE∥AB,
∴∠ABD=∠BDE,
∴∠DBE=∠BDE,
∴BE=DE,
∴BE=AF;
(2)如图,∵EF∥AC,
∴AF:AB=DM:BD,
∵AF=DE,
∴DE:AB=DM:BD,
∵DE∥AB,
∴DE:AB=DN:BN,
∴DM:BD=DN:BN,
即BN•MD=BD•ND.
点评 本题考查了相似三角形的判定与性质:两个三角形相似对应角相等,对应边的比相等.在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用.解决本题的关键是灵活应用平行线分线段成比例定理.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
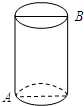 如图所示,有一个圆柱体,高为12cm,底面半径为3cm,在圆柱下底面A处有一只蜘蛛.它想到上底面B处捉住一只苍蝇,则蜘蛛所走的最短路线长应为多少cm(π取3.0).
如图所示,有一个圆柱体,高为12cm,底面半径为3cm,在圆柱下底面A处有一只蜘蛛.它想到上底面B处捉住一只苍蝇,则蜘蛛所走的最短路线长应为多少cm(π取3.0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
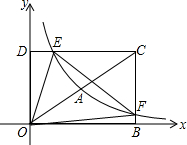 如图,在平面直角坐标系xOy中,矩形OBCD的顶点B,D的坐标分别为(8,0),(0,4).若反比例函数y=$\frac{{k}_{1}}{x}$(x>0)的图象经过对角线OC的中点A,分别交DC边于点E,交BC边于点F.设直线EF的函数表达式为y=k2x+b.
如图,在平面直角坐标系xOy中,矩形OBCD的顶点B,D的坐标分别为(8,0),(0,4).若反比例函数y=$\frac{{k}_{1}}{x}$(x>0)的图象经过对角线OC的中点A,分别交DC边于点E,交BC边于点F.设直线EF的函数表达式为y=k2x+b.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
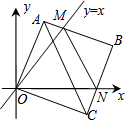 在平面直角坐标系中,边长为3的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上,点O在原点.现将正方形OABC绕O点顺时针旋转,当A点第一次落在直线y=x上时停止旋转,旋转过程中,AB边交直线y=x于点M,BC边交x轴于点N(如图).在旋转正方形OABC的过程中,△MBN的周长为6.
在平面直角坐标系中,边长为3的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上,点O在原点.现将正方形OABC绕O点顺时针旋转,当A点第一次落在直线y=x上时停止旋转,旋转过程中,AB边交直线y=x于点M,BC边交x轴于点N(如图).在旋转正方形OABC的过程中,△MBN的周长为6.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
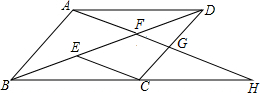 如图,在四边形ABCD中,AB∥DC,E、F为对角线BD上两点,且BE=DF,AF∥EC.
如图,在四边形ABCD中,AB∥DC,E、F为对角线BD上两点,且BE=DF,AF∥EC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
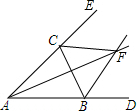 如图,△ABC外角∠CBD,∠BCE的平分线BF、CF相交于点F,则下列结论成立的是( )
如图,△ABC外角∠CBD,∠BCE的平分线BF、CF相交于点F,则下列结论成立的是( )| A. | AF平分BC | B. | AF⊥BC | C. | AF平分∠BAC | D. | AF平分∠BFC |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com