
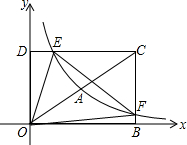
 如图,在平面直角坐标系xOy中,矩形OBCD的顶点B,D的坐标分别为(8,0),(0,4).若反比例函数y=$\frac{{k}_{1}}{x}$(x>0)的图象经过对角线OC的中点A,分别交DC边于点E,交BC边于点F.设直线EF的函数表达式为y=k2x+b.
如图,在平面直角坐标系xOy中,矩形OBCD的顶点B,D的坐标分别为(8,0),(0,4).若反比例函数y=$\frac{{k}_{1}}{x}$(x>0)的图象经过对角线OC的中点A,分别交DC边于点E,交BC边于点F.设直线EF的函数表达式为y=k2x+b.分析 (1)求出点A坐标代入y=$\frac{{k}_{1}}{x}$即可解决.
(2)根据一次函数的图象在反比例函数图象的下面,即可写出不等式的解集.
(3)如图作EM⊥OB于M,利用翻折不变性,设设PC=PN=x,利用△EMN∽△NBP得$\frac{PN}{EN}$=$\frac{PB}{MN}$,求出x即可解决问题.
解答 解:(1)∵四边形OBCD是矩形,
∴OD=BC=4,OB=CD=8,
∵OA=OC,
∴点A坐标(4,2),
∵点A在反比例函数y=$\frac{{k}_{1}}{x}$上,
∴k1=8,
∴反比例函数为y=$\frac{8}{x}$,
故答案为y=$\frac{8}{x}$.
(2)∵点E、F在反比例函数图象上,
∴点E坐标(2,4),点F坐标(8,1),设直线EF为y=kx+b,则$\left\{\begin{array}{l}{2k+b=4}\\{8k+b=1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=5}\end{array}\right.$,
∴直线EF为y=-$\frac{1}{2}$x+5,
于图象可知不等式k2x+b<$\frac{{K}_{1}}{x}$的解集为x<2或x>8.
(3)如图作EM⊥OB于M,
∵∠DOM=∠EMO=∠EDO=90°,
∴四边形DEMO是矩形,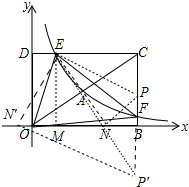
∴EM=DO=4,
∵△EPN是由△EPC翻折得到,
∴EC=EN=6,PC=PN,∠ECP=∠ENP=90°,设PC=PN=x,MN=$\sqrt{E{N}^{2}-E{M}^{2}}$=2$\sqrt{5}$,
∵∠ENM+∠PNB=90°,∠PNB+∠NPB=90°,
∴∠ENM=∠NPB,∵∠EMN=∠PBN,
∴△EMN∽△NBP,
∴$\frac{PN}{EN}$=$\frac{PB}{MN}$,
∴$\frac{x}{6}$=$\frac{4-x}{2\sqrt{5}}$,
∴x=9-3$\sqrt{5}$,
∴PB=BC-PC=4-(9-3$\sqrt{5}$)=3$\sqrt{5}$-5.
当点P′在CB延长线上时,由△EMN′∽△N′BP′,设P′B=x,
∵$\frac{P′N′}{EN′}$=$\frac{P′B}{MN′}$,
∴$\frac{4+x}{6}$=$\frac{x}{2\sqrt{5}}$,
∴x=3$\sqrt{5}$+5,此时点P坐标(8,-3$\sqrt{5}$-5)
故答案为(8,3$\sqrt{5}$-5)或(8,-3$\sqrt{5}$-5))
点评 本题考查反比例函数、一次函数的有关知识、翻折变换等知识,解题的关键是添加辅助线构造相似三角形,学会待定系数法确定函数解析式,学会利用函数图象确定自变量的取值范围,属于中考压轴题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABC中,∠BAC=90°,∠C=30°,以边上AC上一点O为圆心,OA为半径作⊙O,⊙O恰好经过边BC的中点D,并与边AC相交于另一点F.
如图,在Rt△ABC中,∠BAC=90°,∠C=30°,以边上AC上一点O为圆心,OA为半径作⊙O,⊙O恰好经过边BC的中点D,并与边AC相交于另一点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,BD是△ABC的角平分线,点E、F分别在边BC、AB上,且DE∥AB,∠DEF=∠A.
如图,BD是△ABC的角平分线,点E、F分别在边BC、AB上,且DE∥AB,∠DEF=∠A.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 166×104 | B. | 1.66×105 | C. | 1.66×106 | D. | 0.166×107 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
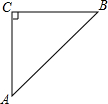 如图,等腰直角△ABC中,AC=BC=$\sqrt{5}$,等腰直角△CDP中,且PB=$\sqrt{2}$.∠CPB=135°,将△CDP绕点C旋转,求BD的长.
如图,等腰直角△ABC中,AC=BC=$\sqrt{5}$,等腰直角△CDP中,且PB=$\sqrt{2}$.∠CPB=135°,将△CDP绕点C旋转,求BD的长.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
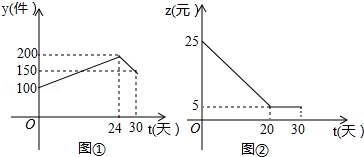
| A. | 第24天的销售量最多 | |
| B. | 20≤t≤30日销售利润不变 | |
| C. | 第30天的日销售利润是750元 | |
| D. | 当0≤t≤24时,设产品日销售量y与时间t的函数关系为y=$\frac{25}{6}$t+100 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com