
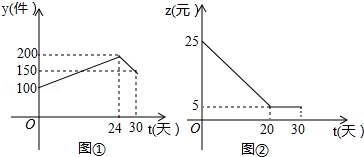
| A�� | ��24������������ | |
| B�� | 20��t��30���������� | |
| C�� | ��30���������������750Ԫ | |
| D�� | ��0��t��24ʱ�����Ʒ��������y��ʱ��t�ĺ�����ϵΪy=$\frac{25}{6}$t+100 |
���� ���ݺ���ͼ��ֱ�����赱0��t��20��һ����Ʒ����������z����λ��Ԫ����ʱ��t����λ���죩�ĺ�����ϵΪz=-x+25����0��t��24ʱ�����Ʒ��������y����λ��������ʱ��t����λ���죩�ĺ�����ϵΪy=$\frac{25}{6}$t+100����������������=����������һ����Ʒ�����������ɽ����жϣ�
��� �⣺A������ͼ�ٿɵõ�24���������Ϊ200��Ϊ��࣬��ԭ����ȷ��
B����20��t��30ʱ�����������仯��һ����Ʒ���������䣬����������仯����ԭ�����
C����30�������������Ϊ��150��5=750��Ԫ������ԭ����ȷ��
D����0��t��24ʱ�����Ʒ��������y����λ��������ʱ��t����λ���죩�ĺ�����ϵΪy=kt+b��
�ѣ�0��100������24��200������ã�$\left\{\begin{array}{l}{b=100}\\{24k+b=200}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{k=\frac{25}{6}}\\{b=100}\end{array}\right.$��
y=$\frac{25}{6}$t+100��ԭ����ȷ��
��ѡ��B��
���� ���⿼����һ�κ�����Ӧ�ã��������Ĺؼ��ǿ��庯��ͼ���ʾ��ʵ�����壬���ô���ϵ������������ʽ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
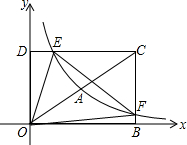 ��ͼ����ƽ��ֱ������ϵxOy�У�����OBCD�Ķ���B��D������ֱ�Ϊ��8��0������0��4����������������y=$\frac{{k}_{1}}{x}$��x��0����ͼ���Խ���OC���е�A���ֱ�DC���ڵ�E����BC���ڵ�F����ֱ��EF�ĺ�������ʽΪy=k2x+b��
��ͼ����ƽ��ֱ������ϵxOy�У�����OBCD�Ķ���B��D������ֱ�Ϊ��8��0������0��4����������������y=$\frac{{k}_{1}}{x}$��x��0����ͼ���Խ���OC���е�A���ֱ�DC���ڵ�E����BC���ڵ�F����ֱ��EF�ĺ�������ʽΪy=k2x+b���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
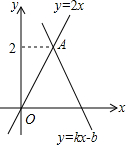 ��ͼ������y=kx+b��k��0����ͼ����B��2��0�����뺯��y=2x��ͼ���ڵ�A����ʽ0��kx+b��2x�Ľ⼯Ϊ��������
��ͼ������y=kx+b��k��0����ͼ����B��2��0�����뺯��y=2x��ͼ���ڵ�A����ʽ0��kx+b��2x�Ľ⼯Ϊ��������| A�� | 1��x��2 | B�� | x��2 | C�� | x��0 | D�� | 0��x��1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
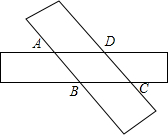 ��ͼ�����ſ�Ϊ1cm�ľ���ֽ��������ţ������ص����ֲ������ı���ABCD��
��ͼ�����ſ�Ϊ1cm�ľ���ֽ��������ţ������ص����ֲ������ı���ABCD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
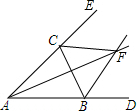 ��ͼ����ABC��ǡ�CBD����BCE��ƽ����BF��CF�ཻ�ڵ�F�������н��۳������ǣ�������
��ͼ����ABC��ǡ�CBD����BCE��ƽ����BF��CF�ཻ�ڵ�F�������н��۳������ǣ�������| A�� | AFƽ��BC | B�� | AF��BC | C�� | AFƽ�֡�BAC | D�� | AFƽ�֡�BFC |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
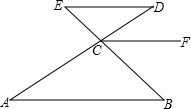 ��ͼ����֪��A=��D����B=��FCB���ܷ�ȷ��ED��CF��λ�ù�ϵ��
��ͼ����֪��A=��D����B=��FCB���ܷ�ȷ��ED��CF��λ�ù�ϵ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com