
(本题10分)如图,在△ABC中,∠ACB=90°,AC=BC,点D在边AB上,连接CD,将线段CD绕点C顺时针旋转90°至CE位置,连接AE.

(1)求证:AB⊥AE;
(2)若BC2=ADAB,求证:四边形ADCE为正方形.
(1)证明见试题解析;(2)证明见试题解析.
【解析】
试题分析:(1)根据旋转的性质得到∠DCE=90°,CD=CE,利用等角的余角相等得∠BCD=∠ACE,然后根据“SAS”可判断△BCD≌△ACE,则∠B=∠CAE=45°,所以∠DAE=90°,即可得到结论;
(2)由于BC=AC,则AC2=ADAB,根据相似三角形的判定方法得到△DAC∽△CAB,则∠CDA=∠BCA=90°,可判断四边形ADCE为矩形,利用CD=CE可判断四边形ADCE为正方形.
解答:证明:(1)∵∠ACB=90°,AC=BC,∴∠B=∠BAC=45°,
∵线段CD绕点C顺时针旋转90°至CE位置,∴∠DCE=90°,CD=CE,
∵∠ACB=90°,∴∠ACB﹣∠ACD=∠DCE﹣∠ACD,即∠BCD=∠ACE,
在△BCD和△ACE中,∵BC=AC,∠BCD=∠ACE,CD=CE,∴△BCD≌△ACE,
∴∠B=∠CAE=45°,∴∠BAE=45°+45°=90°,∴AB⊥AE;
(2)∵BC2=ADAB,而BC=AC,∴AC2=ADAB,
∵∠DAC=∠CAB,∴△DAC∽△CAB,∴∠CDA=∠BCA=90°,
而∠DAE=90°,∠DCE=90°,∴四边形ADCE为矩形,
∵CD=CE,∴四边形ADCE为正方形.
考点:1.旋转的性质;2.全等三角形的判定与性质;3.相似三角形的判定与性质.
考点分析: 考点1:图形的平移与旋转 定义:

科目:初中数学 来源:2014-2015学年湖北省九年级3月联考数学试卷(解析版) 题型:解答题
(本题10分)我区某电子器件厂商投产一种新型电子产品,每件制造成本为18元,在试销过程中发现,每月销售量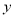 (万件)与销售单价
(万件)与销售单价 (元)之间的关系可以近似地看作一次函数
(元)之间的关系可以近似地看作一次函数 .(利润=售价﹣制造成本)
.(利润=售价﹣制造成本)
(1)写出每月的总利润 (万元)与销售单价
(万元)与销售单价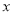 (元)之间的函数关系式;(3分)
(元)之间的函数关系式;(3分)
(2)当销售单价为多少元时,厂商每月能获得350万元的利润?当销售单价为多少元时,厂商每月能获得最大利润?最大利润是多少?(4分)
(3)根据相关部门规定,这种电子产品的销售单价不能高于32元,如果厂商要获得每月不低于350万元的利润,那么制造出这种产品每月的最低制造成本需要多少万元?(3分)
查看答案和解析>>
科目:初中数学 来源:2014-2015学年辽宁省丹东市九年级上学期第一次月考数学试卷(解析版) 题型:选择题
如果x=4是一元二次方程x-3x=a的一个根,则常数a的值是( )
A、2 B、﹣2 C、±2 D、±4
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省泰州市高港实验学校九年级上学期期中考试数学试卷(解析版) 题型:解答题
(本题共10分) 已知关于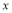 的方程
的方程 ,
,
(1)若 =1是此方程的一根,求
=1是此方程的一根,求 的值及方程的另一根;
的值及方程的另一根;
(2)试说明无论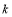 取什么实数值,此方程总有实数根.
取什么实数值,此方程总有实数根.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省七年级上学期第一次质检数学试卷(解析版) 题型:解答题
(1)画出数轴,并用数轴上的点表示下列各数:
-5,2.5,3,-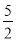 ,0,-3,3
,0,-3,3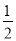 .
.
(2)用“<”号把各数从小到大连起来:
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市锡山区七年级上学期期中考试数学试卷(解析版) 题型:选择题
如果单项式-xa+1y3与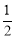 x2yb是同类项,那么a、b的值分别为( )
x2yb是同类项,那么a、b的值分别为( )
A.a=2,b=3 B.a=1,b=2 C.a=1,b =3 D.a=2,b=2
=3 D.a=2,b=2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com