
【题目】(问题背景)
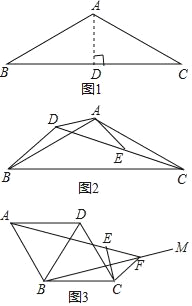
如图1,等腰△ABC中,AB=AC,∠BAC=120°,作AD⊥BC于点D,则D为BC的中点,∠BAD=![]() ∠BAC=60°,
∠BAC=60°,![]() .
.
(问题应用)
如图2,△ABC和△ADE都是等腰三角形,∠BAC=∠DAE=120°,D、E、C三点共线,连接BD,
(1)求证:△ADB≌△AEC;
(2)直接写出AD、BD、CD之间的数量关系;
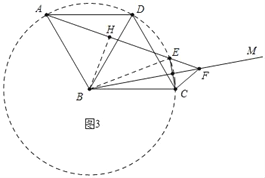
如图3,菱形ABCD中,∠ABC=120°,在△ABC内部作射线BM,作点C关于BM的对称点E,连接AE并延长交BM于点F,连接CE、CF.
(1)判断△EFC的形状,并给出证明.
(2)若AE=5,CE=2,求BF的长.
【答案】【问题应用】(1)见解析;(2)结论:CD=![]() AD+BD,理由见解析;如图3,(1)见解析;(2)BF=3
AD+BD,理由见解析;如图3,(1)见解析;(2)BF=3![]() .
.
【解析】
如图2,(1)只要证明∠DAB=∠CAE,即可根据SAS解决问题;
(2)结论:CD=![]() AD+BD.如图2﹣1中,作AH⊥CD于H,由△DAB≌△EAC,可知BD=CE,在Rt△ADH中,DH=ADcos30°=
AD+BD.如图2﹣1中,作AH⊥CD于H,由△DAB≌△EAC,可知BD=CE,在Rt△ADH中,DH=ADcos30°=![]() AD,由AD=AE,AH⊥DE,推出DH=HE,由CD=DE+EC=2DH+BD=
AD,由AD=AE,AH⊥DE,推出DH=HE,由CD=DE+EC=2DH+BD=![]() AD+BD,即可解决问题;
AD+BD,即可解决问题;
如图3,(1)作BH⊥AE于H,连接BE.由BC=BE=BD=BA,FE=FC,推出A、D、E、C四点共圆,推出∠ADC=∠AEC=120°,推出∠FEC=60°,推出△EFC是等边三角形;
(2)由AE=5,EC=EF=2,推出AH=HE=2.5,FH=4.5,在Rt△BHF中,由∠BFH=30°,可得![]() =cos30°,由此即可解决问题.
=cos30°,由此即可解决问题.
解:【问题应用】如图2,(1)
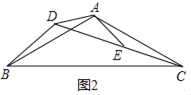
∵∠BAC=∠DAE=120°,
∴∠DAB=∠CAE,
在△DAE和△EAC中,
∵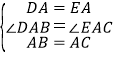 ,
,
∴△DAB≌△EAC,
(2)结论:CD=![]() AD+BD.
AD+BD.
理由:如图2﹣1中,作AH⊥CD于H.
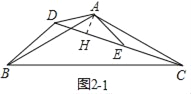
∵△DAB≌△EAC,
∴BD=CE,
在Rt△ADH中,DH=ADcos30°=![]() AD,
AD,
∵AD=AE,AH⊥DE,
∴DH=HE,
∵CD=DE+EC=2DH+BD=![]() AD+BD.
AD+BD.
如图3,(1)证明:如图3中,作BH⊥AE于H,连接BE.
∵四边形ABCD是菱形,∠ABC=120°,
∴△ABD,△/span>BDC是等边三角形,
∴BA=BD=BC,
∵E、C关于BM对称,
∴BC=BE=BD=BA,FE=FC,
∴A、D、E、C四点共圆,
∴∠ADC=∠AEC=120°,
∴∠FEC=60°,
∴△EFC是等边三角形,
(2)∵AE=5,EC=EF=2,
∴AH=HE=2.5,FH=4.5,
在Rt△BHF中,∵∠BFH=30°,
∴![]() =cos30°,
=cos30°,
∴BF=![]() =3
=3![]() .
.
故答案为:【问题应用】(1)见解析;(2)结论:CD=![]() AD+BD,理由见解析;如图3,(1)见解析;(2)BF=3
AD+BD,理由见解析;如图3,(1)见解析;(2)BF=3![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,AB=AC,BE⊥AC于点E,CF⊥AB于点F,BE,CF交于点D,则下列结论中不正确的是( )

A. △ABE≌△ACF B. 点D在∠BAC的平分线上
C. △BDF≌△CDE D. D是BE的中点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了测量山顶铁塔AE的高,小明在27m高的楼CD底部D测得塔顶A的仰角为45°,在楼顶C测得塔顶A的仰角36°52′.已知山高BE为56m,楼的底部D与山脚在同一水平线上,求该铁塔的高AE.(参考数据:sin36°52′≈0.60,tan36°52′≈0.75)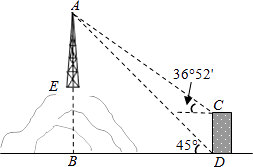
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x、y的方程组![]() ,其中﹣3≤a≤1,给出下列结论:
,其中﹣3≤a≤1,给出下列结论:
①![]() 是方程组的解;
是方程组的解;
②当a=﹣2时,x+y=0;
③若y≤1,则1≤x≤4;
④若S=3x﹣y+2a,则S的最大值为11.
其中正确的有_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将下列各数填入相应的集合内:
3.1415926,﹣2.1,|﹣![]() |, 0,
|, 0, ![]() , -2.626626662…,
, -2.626626662…,![]() ,
, ![]() .
.
正数集合:{ …}
负数集合:{ …}
有理数集合:{ …}
无理数集合:{ …}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】黄石市在创建国家级文明卫生城市中,绿化档次不断提升.某校计划购进A,B两种树木共100棵进行校园绿化升级,经市场调查:购买A种树木2棵,B种树木5棵,共需600元;购买A种树木3棵,B种树木1棵,共需380元.
(1)求A种,B种树木每棵各多少元?
(2)因布局需要,购买A种树木的数量不少于B种树木数量的3倍.学校与中标公司签订的合同中规定:在市场价格不变的情况下(不考虑其他因素),实际付款总金额按市场价九折优惠,请设计一种购买树木的方案,使实际所花费用最省,并求出最省的费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如下表:
X | ﹣1 | 0 | 1 | 3 |
y | ﹣1 | 3 | 5 | 3 |
下列结论:
①ac<0;
②当x>1时,y的值随x值的增大而减小.
③3是方程ax2+(b﹣1)x+c=0的一个根;
④当﹣1<x<3时,ax2+(b﹣1)x+c>0.
其中正确的个数为( )
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 “低碳生活,绿色出行”是我们倡导的一种生活方式,有关部门抽样调查了某单位员工上下班的交通方式,绘制了如下统计图:

(1)填空:样本中的总人数为 ;开私家车的人数m= ;扇形统计图中“骑自行车”所在扇形的圆心角为 度;
(2)补全条形统计图;
(3)该单位共有2000人,积极践行这种生活方式,越来越多的人上下班由开私家车改为骑自行车.若步行,坐公交车上下班的人数保持不变,问原来开私家车的人中至少有多少人改为骑自行车,才能使骑自行车的人数不低于开私家车的人数?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com