
【题目】如图,已知点C在线段AB上,线段AC=10 cm,BC=4 cm,取线段AC、BC的中点D、E.
![]()
(1)请你计算线段DE的长是多少?
(2)观察DE的大小与线段AB的关系,你能用一句简洁的话将这种关系表述出来吗?
(3)若点C为直线AB上的一点,其他条件不变,线段DE的长会改变吗?如果改变,请你求出DE的长.
【答案】(1)DE=7cm;(2)DE=![]() AB,即:线段上任一点把线段分成两部分,这两部分中点间的距离等于原线段长度的一半;(3)线段DE的长会改变,DE的长为7 cm或3 cm.
AB,即:线段上任一点把线段分成两部分,这两部分中点间的距离等于原线段长度的一半;(3)线段DE的长会改变,DE的长为7 cm或3 cm.
【解析】
(1)根据线段中点的定义得到DC=![]() AC,CE=
AC,CE=![]() BC,结合已知即可求出DE;
BC,结合已知即可求出DE;
(2)根据(1)中所求得结果,将这种关系表述出来即可;
(3)分两种情况讨论:①当点C在线段AB上时,②当点C在线段AB延长线上时,根据线段中点的定义和线段和差求出DE的长即可.
解:(1)∵AC=10 cm,BC=4 cm,
∴AB=AC+BC=14cm,
∵点D是线段AC的中点,点E是线段BC的中点,
∴DC=![]() AC,CE=
AC,CE=![]() BC,
BC,
∴DE=DC+CE=![]() AC+
AC+![]() BC=
BC=![]() (AC+BC)=
(AC+BC)=![]() AB=7cm;
AB=7cm;
(2)由(1)可知DE=![]() AB,即:线段上任一点把线段分成两部分,这两部分中点间的距离等于原线段长度的一半;
AB,即:线段上任一点把线段分成两部分,这两部分中点间的距离等于原线段长度的一半;
(3)线段DE的长会改变,
分两种情况讨论:
①当点C在线段AB上时,由(1)可知DE=![]() AB=7cm;
AB=7cm;
②当点C在线段AB延长线上时(如图),
![]()
![]() cm.
cm.
∴DE的长为7 cm或3 cm.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
【题目】股民小杨上星期五买进某公司股票 1000 股,每股 27 元.下表为本周内每日该股票的涨跌情况(单位:元):

(1)星期三收盘时,该股票涨或跌了多少元?
(2)本周内该股票的最高价是每股多少元?最低价是每股多少元?
(3)已知小杨买进股票时付了 1.5‰的手续费,卖出时还需要付成交额的 1.5‰的手续费和 1‰的交易税.如果小杨在星期五收盘前将全部股票卖出,则他的收益情况如何?
(收益=卖股票收入﹣买股票支出﹣卖股票手续费和交易税﹣买股票手续费)
查看答案和解析>>
科目:初中数学 来源: 题型:
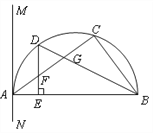
【题目】如图,△ABC内接于半圆,AB是直径,过A作直线MN,若∠MAC=∠ABC.
(1)求证:MN是半圆的切线;
(2)设D是弧AC的中点,连结BD交AC 于G,过D作DE⊥AB于E,交AC于F.求证:FD=FG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A、B在数轴上分别表示数a,b.若A、B两点间的距离记为d,则d和a,b之间的数量关系是d=|a-b|.
(1)数轴上有理数x与有理数-2所对应两点之间的距离可以表示为______;
(2)|x+6|可以表示数轴上有理数x与有理数_______所对应的两点之间的距离;
若|x+6|= |x -2|,则x=______;
(3)若a=1,b=-2,将数轴折叠,使得A点与﹣7表示的点重合,则B点与数______表示的点P重合;
(4)若数轴上M、N两点之间的距离为11(M在N的左侧),且M、N两点经过(3)中折叠后互相重合,则M、N两点表示的数分别是:M:_____, N:_______;
(5)在题(3)的条件下,点A为定点,点B、P为动点,若移动点B、P中一点后,能否使相邻两点间距离相等?若能,请写出移动方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 中,点
中,点![]() 是边
是边![]() 上异于点
上异于点![]() 的一点,
的一点,![]() 的垂直平分线分别交
的垂直平分线分别交![]() 、
、![]() 于
于![]() ,连
,连![]() .
.
(1)求证:![]() ;
;
(2)请求出:![]() 的度数;
的度数;
(3)试猜想线段![]() 之间的数量关系并说明理由.
之间的数量关系并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习完《有理数》后,小奇对运算产生了浓厚的兴趣.借助有理数的运算,定义了一种新运算“⊕”,规则如下:a⊕b=a×b+2×a.
(1)求2⊕(﹣1)的值;
(2)求﹣3⊕(﹣4⊕![]() )的值;
)的值;
(3)试用学习有理数的经验和方法来探究这种新运算“⊕”是否具有交换律?请写出你的探究过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD的对角线AC、BD交于点O,AE平分![]() 交BC于点E,且
交BC于点E,且![]() ,
, ![]() ,连接OE.下列结论:①
,连接OE.下列结论:①![]() ;②SABCD=ABAC;③OB=AB;④
;②SABCD=ABAC;③OB=AB;④![]() ,成立的个数有_________个.
,成立的个数有_________个.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料并解决有关问题:
我们知道:|x|= .现在我们可以用这一结论来化简含有绝对值的代数式,现在我们可以用这一结论来化简含有绝对值的代数式,如化简代数式|x+1|+|x﹣2|时,可令x+1=0和x﹣2=0,分别求得x=﹣1,x=2(称﹣1,2分别为|x+1|与|x﹣2|的零点值).在实数范围内,零点值x=﹣1和,x=2可将全体实数分成不重复且不遗漏的如下3种情况:
.现在我们可以用这一结论来化简含有绝对值的代数式,现在我们可以用这一结论来化简含有绝对值的代数式,如化简代数式|x+1|+|x﹣2|时,可令x+1=0和x﹣2=0,分别求得x=﹣1,x=2(称﹣1,2分别为|x+1|与|x﹣2|的零点值).在实数范围内,零点值x=﹣1和,x=2可将全体实数分成不重复且不遗漏的如下3种情况:
①x<﹣1;②﹣1≤x<2;③x≥2.
从而化简代数式|x+1|+|x﹣2|可分以下3种情况:
①当x<﹣1时,原式=﹣(x+1)﹣(x﹣2)=﹣2x+1;
②当﹣1≤x<2时,原式=x+1﹣(x﹣2)=3;
③当x≥2时,原式=x+1+x﹣2=2x﹣1.综上讨论,原式= .
.
通过以上阅读,请你解决以下问题:
(1)化简代数式|x+2|+|x﹣4|.
(2)求|x﹣1|﹣4|x+1|的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某区初中生一周课外阅读时长的情况,随机抽取部分中学生进行调查,根据调查结果,将阅读时长分为四类:2小时以内,2~4小时(含2小时),4~6小时(含4小时),6小时及以上,并绘制了如图所示不完整的统计图.

(1)本次调查共随机抽取了 名学生;
(2)补全条形统计图;
(3)扇形统计图中,课外阅读时长“4~6小时”对应的圆心角度数为 ![]() ;
;
(4)若该区共有10 000名初中生,估计该地区中学生一周课外阅读时长不少于4小时的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com