
如图1,已知△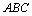 中,
中,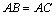 ,现在△
,现在△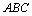 外作∠
外作∠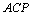 =∠
=∠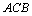 ,在
,在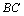 上取一点
上取一点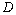 ,在
,在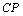 上取一点
上取一点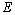 ,使
,使 ,并连接
,并连接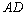 ,
,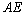 .
.
(1)求证: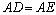 ;
;
(2)若∠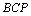 =144°,求∠
=144°,求∠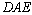 的度数;
的度数;
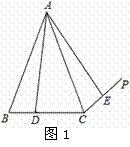
(3)如图2,若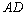 ⊥
⊥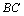
 ,过点
,过点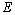 作
作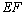 ∥
∥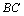 交
交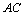 于点
于点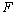 ,连接
,连接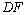
 .试判断四边形
.试判断四边形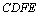 的形状,并给出证明.
的形状,并给出证明.

证明:(1)∵AB=AC,∴∠B=∠ACB,又∵∠ACP=∠ACB,∴∠B=∠ACP,
在△ABD和△ACE中,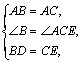 ∴△ABD
∴△ABD ≌△ACE,∴AD=AE;
≌△ACE,∴AD=AE;
(2)∵∠B=∠ACB=∠ACP,∠BCP=144°,∴∠B=∠ACB=∠ACP=72°,
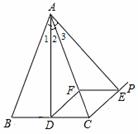 ∴∠BAC=36°,
∴∠BAC=36°,
由(1)知,△ABD≌△ACE,∴∠BAD=∠CAE,
∴∠BAD+∠DAC=∠CAE+∠DAC,即∠DAE=∠BAC=36°. ………………8分
(3)四边形CDFE 为菱形.理由如下:
∵AB=AC,AD⊥BC,∴BD=CD,∠1=∠2,
又∵BD=CE,∴CE=CD,
由(1)知,△ABD≌△ACE,
∴∠1=∠3,∴∠2=∠3,
在△ADF和△AEF中, ∴△ADF≌△AEF,∴DF=EF,
∴△ADF≌△AEF,∴DF=EF,
∵EF∥BC,∴∠EFC=∠DCF,∴∠EFC=∠ECF,∴EC=EF,∴CD=CE=EF=DF,
∴四边形CDFE为菱形.
(注:利用其他方法证明,只要正确即可) 分


科目:初中数学 来源: 题型:
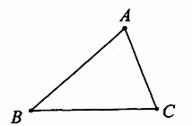
如图,已知△ABC
(1)画出△ABC的中线AD;
(2)在图中分别画出△ABD的高BE,△ACD的高CF;
(3)图中BE,CF的位置关系是______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
某宾馆有单人间和双人间两种房间,入住3个单人间和6个双人间共需1020元,入住1个单人间和5个双人间共需700元,则入住单人间和双人间各5个共需 元.
查看答案和解析>>
科目:初中数学 来源: 题型:
|
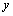 ,运动时间为
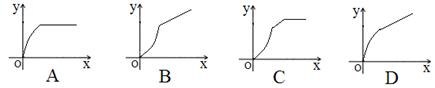
,运动时间为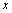 ,则下列图象中能大致表示
,则下列图象中能大致表示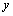 与
与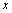 之间函数关系图象的是:
之间函数关系图象的是:
| |
查看答案和解析>>
科目:初中数学 来源: 题型:
将正整数按如图所示的规律排列下去.若用有序实数对(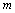 ,
,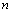 )表示第
)表示第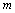 排、从左到右第
排、从左到右第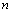 个数,如(3,2)表示实数5.
个数,如(3,2)表示实数5.

(1)图中(7,3)位置上的数 ;数据45对应的有序实数对是 .
(2)第2n行的最后一个数为 , 并简要说明理由.
并简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在正方形ABCD中,等边三角形DEF的顶点E、F分别在AB和BC上。
(1)求证:BE=BF;
(2)若等边三角形DEF的边长为2,求正方形ABCD的周长。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com