
【题目】阅读新知:移项且合并同类项之后,只含有偶次项的四次方程称作双二次方程.其一般形式为ax4+bx2+c=0(a≠0),一般通过换元法解之,具体解法是设 x2=y,则原四次方程化为一元二次方程:ay2+by+c=0,解出y之后代入x2=y,从而求出x的值.
例如解:4x4-8x2+3=0
解:设x2=y,则原方程可化为:4y2-8y+3=0
∵a=4,b=-8,c=3
∴b2-4ac=(-8)2-4×4×3=16>0
∴y=![]() =
=![]()
∴y1=![]() , y2=
, y2=![]()
∴当y1=![]() 时,x2=
时,x2=![]() . ∴x1=
. ∴x1=![]() ,x2=-
,x2=-![]() ;
;
当y1=![]() 时,x2=
时,x2=![]() . ∴x3=
. ∴x3=![]() ,x4=-
,x4=-![]() .
.
小试牛刀:请你解双二次方程:x4-2x2-8=0
归纳提高:
思考以上解题方法,试判断双二次方程的根的情况,下列说法正确的是____________(选出所有的正确答案)
①当b2-4ac≥0时,原方程一定有实数根;
②当b2-4ac<0时,原方程一定没有实数根;
③当b2-4ac≥0,并且换元之后的一元二次方程有两个正实数根时,原方程有4个实数根,换元之后的一元二次方程有一个正实数根一个负实数根时,原方程有2个实数根;
④原方程无实数根时,一定有b2-4ac<0.
【答案】x1=-2,x2=2;②③
【解析】试题分析:先设y=x2,则原方程变形为y2-2y-8=0,运用因式分解法解得y1=-2,y2=4,再把y=-2和4分别代入y=x2得到关于x的一元二次方程,然后解两个一元二次方程,最后确定原方程的解.
根据阅读新知和小试牛刀即可判断①②③④.
试题解析:x4-2x2-8=0
设y=x2,则原方程变为:y2-2y-8=0.
分解因式,得(y+2)(y-4)=0,
解得,y1=-2,y2=4,
当y=-2时,x2=-2,x2+2=0,△=0-4×2<0,此方程无实数解;
当y=4时,x2=4,解得x1=-2,x2=2,
所以原方程的解为x1=-2,x2=2.
根据阅读新知和小试牛刀即可判断②③;
如:x4+4x2+3=0,虽然△=b2-4ac=16-12=4>0,但原方程可化为(x2+1)(x2+3)=0,明显,此方程无解;
所以,①④错误,
故答案为②③.
【方法总结】本题考查了换元法解一元二次方程:当所给方程是双二次方程时,可考虑用换元法降次求解.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】我们美丽的铁一中校园环境优美,文化氛围浓郁,占地70余亩,建筑面积约5万平方米,请将5万平方米这个数用科学记数法表示( )
A.5.0×105平方米
B.5.0×104平方米
C.50×103平方米
D.0.5×106平方米
查看答案和解析>>
科目:初中数学 来源: 题型:
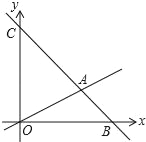
【题目】如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点M在线段OA和射线AC上运动.
(1)求直线AB的解析式.
(2)求△OAC的面积.
(3)是否存在点M,使△OMC的面积是△OAC的面积的![]() ?若存在求出此时点M的坐标;若不存在,说明理由.
?若存在求出此时点M的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=6,BC=8.动点P从点A开始沿折线AC-CB-BA运动,点P在AC,CB,BA边上运动的速度分别为每秒3,4,5个单位.直线l从与AC重合的位置开始,以每秒![]() 个单位的速度沿CB方向移动,移动过程中保持l∥AC,且分别与CB,AB边交于E,F两点,点P与直线l同时出发,设运动的时间为t秒,当点P第一次回到点A时,点P和直线l同时停止运动.
个单位的速度沿CB方向移动,移动过程中保持l∥AC,且分别与CB,AB边交于E,F两点,点P与直线l同时出发,设运动的时间为t秒,当点P第一次回到点A时,点P和直线l同时停止运动.
(1)当t=5秒时,点P走过的路径长为_________;当t=_________秒时,点P与点E重合;
(2)当点P在AC边上运动时,连结PE,并过点E作AB的垂线,垂足为H. 若以C、P、E为顶点的三角形与△EFH相似,试求线段EH的值;
(3)当点P在折线AC-CB-BA上运动时,作点P关于直线EF的对称点Q.在运动过程中,若形成的四边形PEQF为菱形,求t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,“和谐号”高铁列车的小桌板收起时近似看作与地面垂直,小桌板的支架底端与桌面顶端的距离OA = 75厘米.展开小桌板使桌面保持水平,此时CB⊥AO,∠AOB =∠ACB = 37°,且支架长OB与桌面宽BC的长度之和等于OA的长度.求小桌板桌面的宽度BC.(参考数据sin37° ≈ 0.6,cos37°≈ 0.8,tan37° ≈ 0.75)


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知E是平行四边形ABCD中BC边的中点,连接AE并延长AE交DC的延长线于点F。
(1)求证:△ABE≌△FCE;
(2)连接AC、BF,若AE=![]() BC,求证:四边形ABFC为矩形;
BC,求证:四边形ABFC为矩形;
(3)在(2)条件下,当△ABC再满足一个什么条件时,四边形ABFC为正方形。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com