
【题目】在矩形ABCD中,AB=1,AD=![]() ,AF平分∠DAB,过C点作CE
,AF平分∠DAB,过C点作CE![]() BD于E,延长AF、EC交于点H,下列结论中:①AF=FH;②B0=BF;③CA=CH;④BE=3ED;正确的个数为( )
BD于E,延长AF、EC交于点H,下列结论中:①AF=FH;②B0=BF;③CA=CH;④BE=3ED;正确的个数为( )
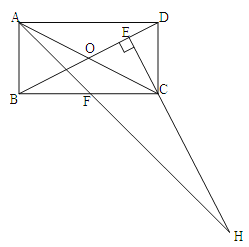
A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】试题分析:根据矩形的性质可得OA=OB=OC=OD,由AD=![]() ,AB=1根据特殊角的锐角三角函数值可求出∠ADB=30°,即得∠ABO=60°,从而可证得△ABO是等边三角形,即得AB=BO=AO=OD=OC=DC,推出BF=AB,求出∠H=∠CAH=15°,求出DE=EO,再依次分析各小题即可作出判断.
,AB=1根据特殊角的锐角三角函数值可求出∠ADB=30°,即得∠ABO=60°,从而可证得△ABO是等边三角形,即得AB=BO=AO=OD=OC=DC,推出BF=AB,求出∠H=∠CAH=15°,求出DE=EO,再依次分析各小题即可作出判断.
根据已知条件不能推出AF=FH,故①错误;
解:∵四边形ABCD是矩形,
∴∠BAD=90°,
∵AD=![]() ,AB=1,
,AB=1,
∴tan∠ADB=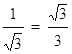 ,
,
∴∠ADB=30°,
∴∠ABO=60°,
∵四边形ABCD是矩形,
∴AD∥BC,AC=BD,AC=2AO,BD=2BO,
∴AO=BO,
∴△ABO是等边三角形,
∴AB=BO,∠AOB=∠BAO=60°=∠COE,
∵AF平分∠BAD,
∴∠BAF=∠DAF=45°,
∵AD∥BC,
∴∠DAF=∠AFB,
∴∠BAF=∠AFB,
∴AB=BF,
∵AB=BO,
∴BF=BO,故②正确;
∵∠BAO=60°,∠BAF=45°,
∴∠CAH=15°,
∵CE⊥BD,
∴∠CEO=90°,
∵∠EOC=60°,
∴∠ECO=30°,
∴∠H=∠ECO-∠CAH=30°-15°=15°=∠CAH,
∴AC=CH,故③正确;
∵△AOB是等边三角形,
∴AO=OB=AB,
∵四边形ABCD是矩形,
∴OA=OC,OB=OD,AB=CD,
∴DC=OC=OD,
∵CE⊥BD,
∴DE=EO=![]() DO=
DO=![]() BD,
BD,
∴BE=3ED,故④正确;
∴正确的有3个,
故选C.


 互动课堂系列答案
互动课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠B=15°,DE垂直平分AB,交BC于点E,垂足为D,若BE=6 cm,则AC等于( )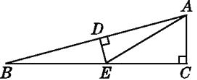
A.6cm
B.5cm
C.4cm
D.3cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图①,在平面直角坐标系xOy中,A(0,5),C(![]() ,0),AOCD为矩形,AE垂直于对角线OD于E,点F是点E关于y轴的对称点,连AF、OF.
,0),AOCD为矩形,AE垂直于对角线OD于E,点F是点E关于y轴的对称点,连AF、OF.
(1)求AF和OF的长;
(2)如图②,将△OAF绕点O顺时针旋转一个角α(0°<α<180°),记旋转中的△OAF为△OA′F′,在旋转过程中,设A′F′所在的直线与线段AD交于点P,与线段OD交于点Q,是否存在这样的P、Q两点,使△DPQ为等腰三角形?若存在,求出此时点P坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,对角线相交于点O;E、F、G、H分别是AD、BD、 BC、AC的中点.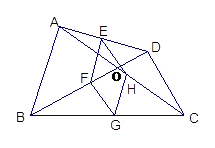
(1)说明四边形EFGH是平行四边形;
(2)当四边形ABCD满足一个什么条件时,四边形EFGH是菱形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,对于平面内任意一点(x,y),若规定以下两种变换:
①f(x,y)=(x+2,y),
②g(x,y)=(﹣x,﹣y),例如按照以上变换有:f(1,1)=(3,1);g(f(1,1))=g(3,1)=(﹣3,﹣1).
则f(g(2,5))=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料,并回答问题
如图,有一根木棒MN放置在数轴上,它的两端M、N分别落在点A、B.将木棒在数轴上水平移动,当点M移动到点B时,点N所对应的数为20,当点N移动到点A时,点M所对应的数为5.
![]() (单位:cm)
(单位:cm)
由此可得,木棒长为__________cm.
借助上述方法解决问题:
一天,美羊羊去问村长爷爷的年龄,村长爷爷说:“我若是你现在这么大,你还要40年才出生呢,你若是我现在这么大,我已经是老寿星了,116岁了,哈哈!”美羊羊纳闷,村长爷爷到底是多少岁?
(1)请你画出示意图,求出村长爷爷和美羊羊现在的年龄.
(2)若羊村中的小羊均与美羊羊同岁,老羊均与村长爷爷同岁。灰太狼计划为全家抓5只羊,综合考虑口感和生长周期等因素,决定所抓羊的年龄之和不超过112岁且高于34岁。请问灰太狼有几种抓羊方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某乡村在开展“美丽乡村”建设时,决定购买A,B两种树苗对村里的主干道进行绿化改造,已知购买A种树苗3棵,B种树苗4棵,需要380元;购买A种树苗5棵,B种树苗2棵,需要400元.
(1)求购买A,B两种树苗每棵各需多少元?
(2)现需购买这两种树苗共100棵,要求购买A种树苗不少于60棵,且用于购买这两种树苗的资金不超过5620元.则有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小区为了绿化环境,计划分两次购进![]() 、
、![]() 两种花草,第一次分别购进
两种花草,第一次分别购进![]() 、
、![]() 两种花草
两种花草![]() 棵和
棵和![]() 棵,共花费
棵,共花费![]() 元;第二次分别购进
元;第二次分别购进![]() 、
、![]() 两种花草
两种花草![]() 棵和
棵和![]() 棵.两次共花费
棵.两次共花费![]() 元(两次购进的
元(两次购进的![]() 、
、![]() 两种花草价格均分别相同).
两种花草价格均分别相同).
(![]() )
)![]() 、
、![]() 两种花草每棵的价格分别是多少元?
两种花草每棵的价格分别是多少元?
(![]() )若购买
)若购买![]() 、
、![]() 两种花草共
两种花草共![]() 棵,且
棵,且![]() 种花草的数量少于
种花草的数量少于![]() 种花草的数量的
种花草的数量的![]() 倍,请你给出一种费用最省的方案,并求出该方案所需费用.
倍,请你给出一种费用最省的方案,并求出该方案所需费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
如图1,在平面直角坐标系xOy中,直线y1=ax+b与双曲线y2=![]() 交于A(1,3)和B(﹣3,﹣1)两点.
交于A(1,3)和B(﹣3,﹣1)两点.
观察图象可知:
①当x=﹣3或1时,y1=y2;
②当﹣3<x<0或x>1时,y1>y2,即通过观察函数的图象,可以得到不等式ax+b>![]() 的解集.
的解集.
有这样一个问题:求不等式x3+4x2﹣x﹣4>0的解集.
某同学根据学习以上知识的经验,对求不等式x3+4x2﹣x﹣4>0的解集进行了探究.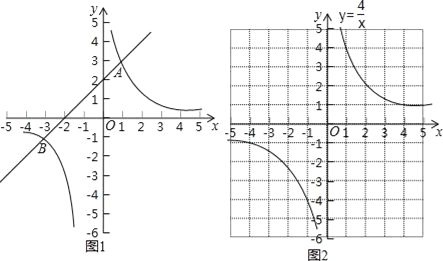
下面是他的探究过程,请将(2)、(3)、(4)补充完整:
(1)将不等式按条件进行转化:
当x=0时,原不等式不成立;
当x>0时,原不等式可以转化为x2+4x﹣1>![]() ;
;
当x<0时,原不等式可以转化为x2+4x﹣1<![]() ;
;
(2)构造函数,画出图象
设y3=x2+4x﹣1,y4=![]() ,在同一坐标系中分别画出这两个函数的图象.
,在同一坐标系中分别画出这两个函数的图象.
双曲线y4=![]() 如图2所示,请在此坐标系中画出抛物线y3=x2+4x﹣1;(不用列表)
如图2所示,请在此坐标系中画出抛物线y3=x2+4x﹣1;(不用列表)
(3)确定两个函数图象公共点的横坐标
观察所画两个函数的图象,猜想并通过代入函数解析式验证可知:满足y3=y4的所有x的值为 ;
(4)借助图象,写出解集
结合(1)的讨论结果,观察两个函数的图象可知:不等式x3+4x2﹣x﹣4>0的解集为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com