
ЁОЬтФПЁПФГаЁЧјЮЊСЫТЬЛЏЛЗОГЃЌМЦЛЎЗжСНДЮЙКНј![]() ЁЂ
ЁЂ![]() СНжжЛЈВнЃЌЕквЛДЮЗжБ№ЙКНј
СНжжЛЈВнЃЌЕквЛДЮЗжБ№ЙКНј![]() ЁЂ
ЁЂ![]() СНжжЛЈВн
СНжжЛЈВн![]() ПУКЭ
ПУКЭ![]() ПУЃЌЙВЛЈЗб
ПУЃЌЙВЛЈЗб![]() дЊЃЛЕкЖўДЮЗжБ№ЙКНј
дЊЃЛЕкЖўДЮЗжБ№ЙКНј![]() ЁЂ
ЁЂ![]() СНжжЛЈВн
СНжжЛЈВн![]() ПУКЭ
ПУКЭ![]() ПУЃЎСНДЮЙВЛЈЗб
ПУЃЎСНДЮЙВЛЈЗб![]() дЊЃЈСНДЮЙКНјЕФ
дЊЃЈСНДЮЙКНјЕФ![]() ЁЂ
ЁЂ![]() СНжжЛЈВнМлИёОљЗжБ№ЯрЭЌЃЉЃЎ
СНжжЛЈВнМлИёОљЗжБ№ЯрЭЌЃЉЃЎ
ЃЈ![]() ЃЉ
ЃЉ![]() ЁЂ
ЁЂ![]() СНжжЛЈВнУППУЕФМлИёЗжБ№ЪЧЖрЩйдЊЃП
СНжжЛЈВнУППУЕФМлИёЗжБ№ЪЧЖрЩйдЊЃП
ЃЈ![]() ЃЉШєЙКТђ
ЃЉШєЙКТђ![]() ЁЂ
ЁЂ![]() СНжжЛЈВнЙВ
СНжжЛЈВнЙВ![]() ПУЃЌЧв
ПУЃЌЧв![]() жжЛЈВнЕФЪ§СПЩйгк
жжЛЈВнЕФЪ§СПЩйгк![]() жжЛЈВнЕФЪ§СПЕФ
жжЛЈВнЕФЪ§СПЕФ![]() БЖЃЌЧыФуИјГівЛжжЗбгУзюЪЁЕФЗНАИЃЌВЂЧѓГіИУЗНАИЫљашЗбгУЃЎ
БЖЃЌЧыФуИјГівЛжжЗбгУзюЪЁЕФЗНАИЃЌВЂЧѓГіИУЗНАИЫљашЗбгУЃЎ
ЁОД№АИЁПЃЈ![]() ЃЉAЃЌBСНжжЛЈВнМлИёЗжБ№ЮЊ20дЊКЭ5дЊЃЛ
ЃЉAЃЌBСНжжЛЈВнМлИёЗжБ№ЮЊ20дЊКЭ5дЊЃЛ
ЃЈ![]() ЃЉЗбгУзюЪЁЕФЗНАИЮЊЙКТђAжжЛЈВн11ПУЃЌЙКТђBжжЛЈВн20ПУЃЌЛЈЗбзюЩйЮЊ320дЊЃЎ
ЃЉЗбгУзюЪЁЕФЗНАИЮЊЙКТђAжжЛЈВн11ПУЃЌЙКТђBжжЛЈВн20ПУЃЌЛЈЗбзюЩйЮЊ320дЊЃЎ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉЩшAжжЛЈВнУППУЕФМлИёxдЊЃЌBжжЛЈВнУППУЕФМлИёyдЊЃЌИљОнЕквЛДЮЗжБ№ЙКНјAЁЂBСНжжЛЈВн30ПУКЭ15ПУЃЌЙВЛЈЗб940дЊЃЛЕкЖўДЮЗжБ№ЙКНјAЁЂBСНжжЛЈВн12ПУКЭ5ПУЃЌСНДЮЙВЛЈЗб675дЊЃЛСаГіЗНГЬзщЃЌМДПЩНтД№ЃЎЃЈ2ЃЉЩшAжжЛЈВнЕФЪ§СПЮЊmжъЃЌдђBжжЛЈВнЕФЪ§СПЮЊЃЈ31-mЃЉжъЃЌИљОнBжжЛЈВнЕФЪ§СПЩйгкAжжЛЈВнЕФЪ§СПЕФ2БЖЃЌЕУГіmЕФЗЖЮЇЃЌЩшзмЗбгУЮЊWдЊЃЌИљОнзмЗбгУ=СНжжЛЈВнЕФЗбгУжЎКЭНЈСЂКЏЪ§ЙиЯЕЪНЃЌгЩвЛДЮКЏЪ§ЕФаджЪОЭПЩвдЧѓГіНсТлЃЎ
ЪдЬтНтЮіЃКЃЈ![]() ЃЉЩш
ЃЉЩш![]() ЃЌ
ЃЌ ![]() СНжжЛЈВнУППУЕФМлИёЗжБ№ЮЊ
СНжжЛЈВнУППУЕФМлИёЗжБ№ЮЊ![]() дЊКЭ
дЊКЭ![]() дЊЃЎ
дЊЃЎ
гЩЬтвтЕУ![]() ЃЌ
ЃЌ
НтЕУЃК ![]() ЃЌ
ЃЌ
Д№ЃК ![]() ЃЌ
ЃЌ ![]() СНжжЛЈВнМлИёЗжБ№ЮЊ
СНжжЛЈВнМлИёЗжБ№ЮЊ![]() дЊКЭ
дЊКЭ![]() дЊЃЎ
дЊЃЎ
ЃЈ![]() ЃЉЩшЙКТђ
ЃЉЩшЙКТђ![]() жжЛЈВн
жжЛЈВн![]() ПУЃЌдђЙКТђ
ПУЃЌдђЙКТђ![]() жжЛЈВнЮЊ
жжЛЈВнЮЊ![]() ПУЃЌ
ПУЃЌ
гЩЬтвтЕУ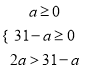 ЃЌЧв
ЃЌЧв![]() ЮЊећЪ§ЃЌ
ЮЊећЪ§ЃЌ
НтЕУЃК ![]() Чв
Чв![]() ЮЊећЪ§ЃЌ
ЮЊећЪ§ЃЌ
гЩЃЈ![]() ЃЉПЩжЊЃЌ
ЃЉПЩжЊЃЌ ![]() ЕФМлИёЮЊ
ЕФМлИёЮЊ![]() дЊ/ПУЃЌ
дЊ/ПУЃЌ ![]() ЕФМлИёЮЊ
ЕФМлИёЮЊ![]() дЊ/ПУЃЌ
дЊ/ПУЃЌ
ЩшЗбгУЮЊ![]() ЃЌ
ЃЌ
дђ![]() ЃЌ
ЃЌ
гЩвЛДЮКЏЪ§ЕФаджЪПЩЕУЃК ![]() Ыц
Ыц![]() ЕФдіДѓЖјдіДѓЃЌ
ЕФдіДѓЖјдіДѓЃЌ
ЁрЕБ![]() ШЁзюаЁећЪ§
ШЁзюаЁећЪ§![]() ЪБЃЌзюаЁжЕЮЊЃК
ЪБЃЌзюаЁжЕЮЊЃК ![]() ЃЌ
ЃЌ
Д№ЃКЗбгУзюЪЁЕФЗНАИЮЊЙКТђ![]() жжЛЈВн
жжЛЈВн![]() ПУЃЌЙКТђ
ПУЃЌЙКТђ![]() жжЛЈВн
жжЛЈВн![]() ПУЃЌЛЈЗбзюЩйЮЊ
ПУЃЌЛЈЗбзюЩйЮЊ![]() дЊЃЎ
дЊЃЎ


 жаПМНтЖСПМЕуОЋСЗЯЕСаД№АИ
жаПМНтЖСПМЕуОЋСЗЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаЫЕЗЈе§ШЗЕФгаЃЈ ЃЉ
ЂйЙ§СНЕужЛФмЛвЛЬѕжБЯп,ЂкЙ§СНЕужЛФмЛвЛЬѕЩфЯп,ЂлЙ§СНЕужЛФмЛвЛЬѕЯпЖЮ
A. 1ИіB. 2ИіC. 3ИіD. 0Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкОиаЮABCDжаЃЌAB=1ЃЌAD=![]() ЃЌAFЦНЗжЁЯDABЃЌЙ§CЕузїCE
ЃЌAFЦНЗжЁЯDABЃЌЙ§CЕузїCE![]() BDгкEЃЌбгГЄAFЁЂECНЛгкЕуHЃЌЯТСаНсТлжаЃКЂйAF=FHЃЛЂкB0=BFЃЛЂлCA=CHЃЛЂмBE=3EDЃЛе§ШЗЕФИіЪ§ЮЊ( )
BDгкEЃЌбгГЄAFЁЂECНЛгкЕуHЃЌЯТСаНсТлжаЃКЂйAF=FHЃЛЂкB0=BFЃЛЂлCA=CHЃЛЂмBE=3EDЃЛе§ШЗЕФИіЪ§ЮЊ( )
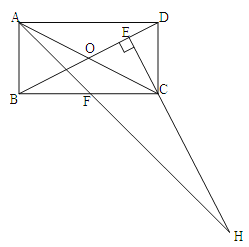
A. 1Иі B. 2Иі C. 3Иі D. 4Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
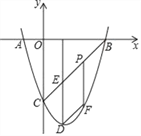
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпy=x2+bx+cгыxжсЯрНЛгкAЁЂBСНЕуЃЌЕуBЕФзјБъЮЊЃЈ3ЃЌ0ЃЉЃЌгыyжсЯрНЛгкЕуCЃЈ0ЃЌЉ3ЃЉЃЌЖЅЕуЮЊDЃЎ
ЃЈ1ЃЉЧѓГіХзЮяЯпy=x2+bx+cЕФБэДяЪНЃЛ
ЃЈ2ЃЉСЌНсBCЃЌгыХзЮяЯпЕФЖдГЦжсНЛгкЕуEЃЌЕуPЮЊЯпЖЮBCЩЯЕФвЛИіЖЏЕуЃЌЙ§ЕуPзїPFЁЮDEНЛХзЮяЯпгкЕуFЃЌЩшЕуPЕФКсзјБъЮЊmЃЎ
ЂйЕБmЮЊКЮжЕЪБЃЌЫФБпаЮPEDFЮЊЦНааЫФБпаЮЃЎ
ЂкЩшЫФБпаЮOBFCЕФУцЛ§ЮЊSЃЌЧѓSЕФзюДѓжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁЯABC=38ЁуЃЌЁЯACB=100ЁуЃЌADЦНЗжЁЯBACЃЌAEЪЧBCБпЩЯЕФИпЃЌЧѓЁЯDAEЕФЖШЪ§ЃЎ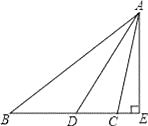
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЁб![]() ЕФАыОЖЮЊ
ЕФАыОЖЮЊ![]() ЃЌ
ЃЌ ![]() ЮЊжБОЖЃЌ
ЮЊжБОЖЃЌ ![]() ЮЊЯвЃЎ
ЮЊЯвЃЎ ![]() гы
гы![]() НЛгкЕу
НЛгкЕу![]() ЃЌНЋ
ЃЌНЋ![]() бизХ
бизХ![]() ЗелКѓЃЌЕу
ЗелКѓЃЌЕу![]() гыдВаФ
гыдВаФ![]() жиКЯЃЌбгГЄ
жиКЯЃЌбгГЄ![]() жС
жС![]() ЃЌЪЙ
ЃЌЪЙ![]() ЃЌСДНг
ЃЌСДНг![]() ЃЎ
ЃЎ
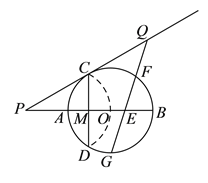
ЃЈ![]() ЃЉЧѓ
ЃЉЧѓ![]() ЕФГЄЃЎ
ЕФГЄЃЎ
ЃЈ![]() ЃЉЧѓжЄЃК
ЃЉЧѓжЄЃК ![]() ЪЧЁб
ЪЧЁб![]() ЕФЧаЯпЃЎ
ЕФЧаЯпЃЎ
ЃЈ![]() ЃЉЕу
ЃЉЕу![]() ЮЊ
ЮЊ![]() ЕФжаЕуЃЌдк
ЕФжаЕуЃЌдк![]() бгГЄЯпЩЯгавЛЖЏЕу
бгГЄЯпЩЯгавЛЖЏЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌНЛ
ЃЌНЛ![]() гкЕу
гкЕу![]() ЃЈ
ЃЈ![]() гы
гы![]() ЁЂ
ЁЂ![]() ВЛжиКЯЃЉЃЎдђ
ВЛжиКЯЃЉЃЎдђ![]() ЮЊвЛЖЈжЕЃЎЧыЫЕУїРэгЩЃЌВЂЧѓГіИУЖЈжЕЃЎ
ЮЊвЛЖЈжЕЃЎЧыЫЕУїРэгЩЃЌВЂЧѓГіИУЖЈжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПГѕШ§ЃЈ1ЃЉАрвЊДгМзЁЂввЁЂБћЁЂЖЁет![]() УћЭЌбЇжаЫцЛњбЁШЁ
УћЭЌбЇжаЫцЛњбЁШЁ![]() УћЭЌбЇВЮМгбЇаЃБЯвЕЩњДњБэзљЬИЛсЃЎЧѓЯТСаЪТМўЕФИХТЪЃК
УћЭЌбЇВЮМгбЇаЃБЯвЕЩњДњБэзљЬИЛсЃЎЧѓЯТСаЪТМўЕФИХТЪЃК
ЃЈ![]() ЃЉвбШЗЖЈМзВЮМгЃЌСэЭт
ЃЉвбШЗЖЈМзВЮМгЃЌСэЭт![]() ШЫЧЁКУбЁжаввЃЛ
ШЫЧЁКУбЁжаввЃЛ
ЃЈ![]() ЃЉЫцЛњбЁШЁ
ЃЉЫцЛњбЁШЁ![]() УћЭЌбЇЃЌЧЁКУбЁжаМзКЭввЃЎ
УћЭЌбЇЃЌЧЁКУбЁжаМзКЭввЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКa2Љ4ab+5b2Љ2b+1=0ЃЌдђвдaЃЌbЮЊИљЕФвЛдЊЖўДЮЗНГЬЮЊ ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ,дкЁїABCжа,AB=AC,EFНЛABгкЕуE,НЛACЕФбгГЄЯпгкЕуF,НЛBCгкЕуD,ЧвBE=CF.
ЧѓжЄ:DE=DF.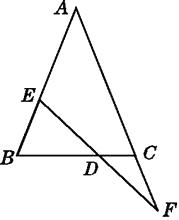
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com