【题目】如图，∠ABC=38°，∠ACB=100°，AD平分∠BAC，AE是BC边上的高，求∠DAE的度数．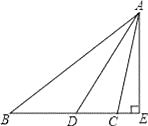
【答案】解：∵∠ABC=38°，∠ACB=100°（己知）
∴∠BAC=180°﹣38°﹣100°=42°（三角形内角和180°）．
又∵AD平分∠BAC（己知），
∴∠BAD=21°，
∴∠ADE=∠ABC+∠BAD=59°（三角形的外角性质）．
又∵AE是BC边上的高，即∠E=90°，
∴∠DAE=90°﹣59°=31°
【解析】由已知和三角形的内角和可求出∠BAC的度数，再由AD平分∠BAC可得∠BAD的度数，从而求出∠ADE的度数，再在△ABE中求出∠DAE的度数.
【考点精析】根据题目的已知条件，利用三角形的内角和外角和三角形的外角的相关知识可以得到问题的答案，需要掌握三角形的三个内角中，只可能有一个内角是直角或钝角；直角三角形的两个锐角互余；三角形的一个外角等于和它不相邻的两个内角的和；三角形的一个外角大于任何一个和它不相邻的内角；三角形一边与另一边的延长线组成的角，叫三角形的外角；三角形的一个外角等于和它不相邻的两个内角的和；三角形的一个外角大于任何一个和它不相邻的内角．
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，对于平面内任意一点（x，y），若规定以下两种变换：
①f（x，y）＝（x+2，y），
②g（x，y）＝（﹣x，﹣y），例如按照以上变换有：f（1，1）＝（3，1）；g（f（1，1））＝g（3，1）＝（﹣3，﹣1）．
则f（g（2，5））＝_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某乡村在开展“美丽乡村”建设时，决定购买A，B两种树苗对村里的主干道进行绿化改造，已知购买A种树苗3棵，B种树苗4棵，需要380元；购买A种树苗5棵，B种树苗2棵，需要400元．
（1）求购买A，B两种树苗每棵各需多少元？
（2）现需购买这两种树苗共100棵，要求购买A种树苗不少于60棵，且用于购买这两种树苗的资金不超过5620元．则有哪几种购买方案？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系xOy中，点A、B的坐标分别为（2，﹣1）、（3，0），以原点O为位似中心，把线段AB放大，点B的对应点B′的坐标为（6，0），则点A的对应点A′的坐标为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某小区为了绿化环境，计划分两次购进
、
两种花草，第一次分别购进
、
两种花草
棵和
棵，共花费
元；第二次分别购进
、
两种花草
棵和
棵．两次共花费
元（两次购进的
、
两种花草价格均分别相同）．
（
）
、
两种花草每棵的价格分别是多少元？
（
）若购买
、
两种花草共
棵，且
种花草的数量少于
种花草的数量的
倍，请你给出一种费用最省的方案，并求出该方案所需费用．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC三个顶点的坐标分别为A（1，1），B（4，2），C（3，4）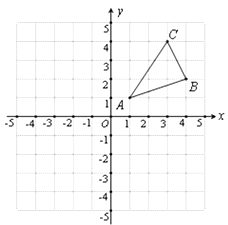
⑴ 作出与△ABC关于y轴对称△A1B1C1 ， 并写出三个顶点的坐标为：A1（），B1（），C1（）；
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
