
【题目】如图,已知⊙![]() 的半径为
的半径为![]() ,
, ![]() 为直径,
为直径, ![]() 为弦.
为弦. ![]() 与
与![]() 交于点
交于点![]() ,将
,将![]() 沿着
沿着![]() 翻折后,点
翻折后,点![]() 与圆心
与圆心![]() 重合,延长
重合,延长![]() 至
至![]() ,使
,使![]() ,链接
,链接![]() .
.
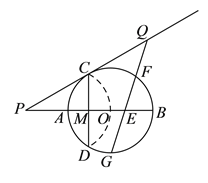
(![]() )求
)求![]() 的长.
的长.
(![]() )求证:
)求证: ![]() 是⊙
是⊙![]() 的切线.
的切线.
(![]() )点
)点![]() 为
为![]() 的中点,在
的中点,在![]() 延长线上有一动点
延长线上有一动点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() (
(![]() 与
与![]() 、
、![]() 不重合).则
不重合).则![]() 为一定值.请说明理由,并求出该定值.
为一定值.请说明理由,并求出该定值.
【答案】(1)![]() ;(2)证明见解析;(3)
;(2)证明见解析;(3)![]() ,理由见解析.
,理由见解析.
【解析】试题分析:(1)连接OC,根据翻折的性质求出OM,CD⊥OA,再利用勾股定理列式求解即可;(2)利用勾股定理列式求出PC,然后利用勾股定理逆定理求出∠PCO=90°,再根据圆的切线的定义证明即可;(3)连接GA、AF、GB,根据等弧所对的圆周角相等可得∠BAG=∠AFG,然后根据两组角对应相等两三角相似求出△AGE和△FGA相似,根据相似三角形对应边成比例可得![]() ,从而得到GEGF=AG2,再根据等腰直角三角形的性质求解即可.
,从而得到GEGF=AG2,再根据等腰直角三角形的性质求解即可.
(![]() )连接
)连接![]() ,
,

∵![]() 沿
沿![]() 翻折后,
翻折后, ![]() 与
与![]() 重合,
重合,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() .
.
(![]() )∵
)∵![]() ,
, ![]() ,
,
∵![]() ,
, ![]() ,
,
∴![]() ,
,
∵![]() ,
, ![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() 是⊙
是⊙![]() 的切线.
的切线.
(![]() )
)![]() ,
, ![]() 为定值,
为定值,
连接![]() ,
, ![]() ,
, ![]() ,
,

∵点![]() 为
为![]() 的中点,
的中点,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() 为直径,
为直径, ![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】阅读材料,并回答问题
如图,有一根木棒MN放置在数轴上,它的两端M、N分别落在点A、B.将木棒在数轴上水平移动,当点M移动到点B时,点N所对应的数为20,当点N移动到点A时,点M所对应的数为5.
![]() (单位:cm)
(单位:cm)
由此可得,木棒长为__________cm.
借助上述方法解决问题:
一天,美羊羊去问村长爷爷的年龄,村长爷爷说:“我若是你现在这么大,你还要40年才出生呢,你若是我现在这么大,我已经是老寿星了,116岁了,哈哈!”美羊羊纳闷,村长爷爷到底是多少岁?
(1)请你画出示意图,求出村长爷爷和美羊羊现在的年龄.
(2)若羊村中的小羊均与美羊羊同岁,老羊均与村长爷爷同岁。灰太狼计划为全家抓5只羊,综合考虑口感和生长周期等因素,决定所抓羊的年龄之和不超过112岁且高于34岁。请问灰太狼有几种抓羊方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
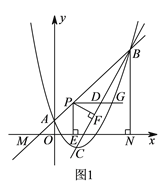
【题目】如图![]() ,二次函数
,二次函数![]() 的图象与一次函数
的图象与一次函数![]() 的图象交于
的图象交于![]() ,
, ![]() 两点,点
两点,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在第一象限内,点
在第一象限内,点![]() 是二次函数图象的顶点,点
是二次函数图象的顶点,点![]() 是一次函数
是一次函数![]() 的图象与
的图象与![]() 轴的交点,过点
轴的交点,过点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,且
,且![]() .
.
(![]() )求直线
)求直线![]() 和直线
和直线![]() 的解析式.
的解析式.
(2)点![]() 是线段
是线段![]() 上一点,点
上一点,点![]() 是线段
是线段![]() 上一点,
上一点, ![]() 轴,射线
轴,射线![]() 与抛物线交于点
与抛物线交于点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,
, ![]() 于点
于点![]() ,当
,当![]() 与
与![]() 的乘积最大时,在线段
的乘积最大时,在线段![]() 上找一点
上找一点![]() (不与点
(不与点![]() ,点
,点![]() 重合),使
重合),使![]() 的值最小,求点
的值最小,求点![]() 的坐标和
的坐标和![]() 的最小值.
的最小值.
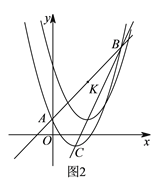
(![]() )如图
)如图![]() ,直线
,直线![]() 上有一点
上有一点![]() ,将二次函数
,将二次函数![]() 沿直线
沿直线![]() 平移,平移的距离是
平移,平移的距离是![]() ,平移后抛物线使点
,平移后抛物线使点![]() ,点
,点![]() 的对应点分别为点
的对应点分别为点![]() ,点
,点![]() ;当
;当![]() 是直角三角形时,求t的值.
是直角三角形时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小区为了绿化环境,计划分两次购进![]() 、
、![]() 两种花草,第一次分别购进
两种花草,第一次分别购进![]() 、
、![]() 两种花草
两种花草![]() 棵和
棵和![]() 棵,共花费
棵,共花费![]() 元;第二次分别购进
元;第二次分别购进![]() 、
、![]() 两种花草
两种花草![]() 棵和
棵和![]() 棵.两次共花费
棵.两次共花费![]() 元(两次购进的
元(两次购进的![]() 、
、![]() 两种花草价格均分别相同).
两种花草价格均分别相同).
(![]() )
)![]() 、
、![]() 两种花草每棵的价格分别是多少元?
两种花草每棵的价格分别是多少元?
(![]() )若购买
)若购买![]() 、
、![]() 两种花草共
两种花草共![]() 棵,且
棵,且![]() 种花草的数量少于
种花草的数量少于![]() 种花草的数量的
种花草的数量的![]() 倍,请你给出一种费用最省的方案,并求出该方案所需费用.
倍,请你给出一种费用最省的方案,并求出该方案所需费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
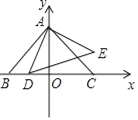
【题目】如图,在平面直角坐标系中,点A(0,2),B(﹣2,0),点D是x轴上一个动点,以AD为一直角边在一侧作等腰直角三角形ADE,∠DAE=90°,若△ABD为等腰三角形时点E的坐标为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一艘轮船和一艘快艇沿相同路线从甲港出发到乙港,行驶过程随时间变化的图象如图所示,下列结论错误的是( )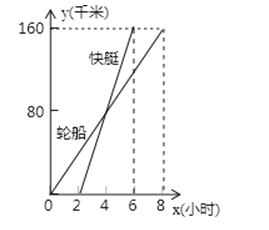
A.轮船的速度为20千米/小时
B.快艇的速度为![]() 千米/小时
千米/小时
C.轮船比快艇先出发2小时
D.快艇比轮船早到2小时
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com