
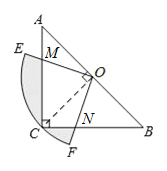
【题目】如图,在△ABC中,∠C=90°,AC=BC,斜边AB=2,O是AB的中点,以O为圆心,线段OC的长为半径画圆心角为90°的扇形OEF,弧EF经过点C,则图中阴影部分的面积为_____.

【答案】![]() .
.
【解析】证明△AMO≌△CNO,将四边形CMON的面积转化为△ACO的面积,即可用割补法求出阴影部分的面积.
因为点O是AB的中点,所以AO=BO=CO,
由勾股定理得AB=![]() .
.
因为∠ACB=90°,∠EOF=90°,所以∠CMO+∠CNO=180°,又∠AMO+∠CMO=180°,所以∠AMO=∠CNO,
又因为∠A=∠B,AO=CO,
所以△AMO≌△CNO.
所以四边形CMON的面积=△CMO的面积+△CNO的面积
=△CMO的面积+△CNO的面积=△ACO的面积=△ABC面积的一半.
所以阴影部分的面积=扇形OEF的面积-四边形CMON的面积
=扇形OEF的面积-△ACO的面积
=![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】下列说法错误的是( )
A.平面内过一点有且只有一条直线与已知直线垂直
B.两点之间的所有连线中,线段最短
C.经过两点有且只有一条直线
D.经过一点有且只有一条直线
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为靓化家园,改善生活环境,我县农村实行垃圾分类集中处理.现某村要清理卫生死角垃圾,若用甲、乙两车运送,两车各运15趟可完成,已知甲、乙两车单独运完此堆垃圾,乙车所运趟数是甲车的3倍.求甲、乙两车单独运完此堆垃圾各需运多少趟?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校团委组织65名新团员为学校建花坛搬砖,女同学每人搬4块砖,男同学每人搬8块砖,总共搬了400块砖.
(1)根据题意,请把表格填完整;
参加年级 | 女同学 | 男同学 | 总数 |
参加人数 | x | 65 | |
每人搬砖 | 4 | 8 | |
共搬砖 | 400 |
(2)问这些新团员中有多少名女同学?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点P位于y轴右侧,距y轴3个单位长度,位于x轴上方,距离x轴4个单位长度,则点P坐标是( )
A.(﹣3,4)
B.(3,4)
C.(﹣4,3)
D.(4,3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校要举办一次演讲比赛,每班只能选一人参加比赛.但八年级一班共有甲、乙两人的演讲水平相不相上下,现要在他们两人中选一人去参加全校的演讲比赛,经班主任与全班同学协商决定用摸小球的游戏来确定谁去参赛(胜者参赛).
游戏规则如下:在两个不透明的盒子中,一个盒子里放着两个红球,一个白球;另一个盒子里放着三个白球,一个红球,从两个盒子中各摸一个球,若摸得的两个球都是红球,甲胜;摸得的两个球都是白球,乙胜,否则,视为平局.若为平局,继续上述游戏,直至分出胜负为止.
根据上述规则回答下列问题:
(1)从两个盒子各摸出一个球,一个球为白球,一个球为红球的概率是多少?
(2)该游戏公平吗?请用列表或树状图等方法说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=A1B,A1C=A1A2,A2D=A2A3,A3E=A3A4,∠B=20°,则∠A4=( )
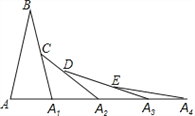
A. 10° B. 15° C. 30° D. 40°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com