
【题目】如图,□ABCD中,BD=2AD , AC交BD于点O , E为OA的中点,M为DC的中点,观察EM与DC的数量关系,并说明你的理由.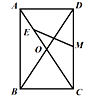
【答案】解:EM=![]() DC
DC
理由:如图:连结 DE.
∵ 四边形ABCD是平行四边形.
∴BD=2OD.
又∵BD=2AD,
∴ AD=OD,
∴ △ADO 为等腰三角形.
又 ∵E为AO 的中点.
∴DE![]() AO.
AO.
△DEC 为直角三角形, CD为斜边.
又 ∵M 为斜边CD 的中点.
∴EM=![]() CD.
CD.
【解析】如图:连结 DE.由平行四边形的性质得BD=2OD.由BD=2AD,得 AD=OD,△ADO为等腰三角形.由其性质得DE![]() AO.由直角三角形中
AO.由直角三角形中
斜边上的中线等于斜边的一半即可。
【考点精析】根据题目的已知条件,利用直角三角形斜边上的中线和平行四边形的性质的相关知识可以得到问题的答案,需要掌握直角三角形斜边上的中线等于斜边的一半;平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.


科目:初中数学 来源: 题型:
【题目】在平行四边形ABCD中添加下列条件,不能判定四边形ABCD是菱形的是( )
A. AB=BC B. AC⊥BD C. AC=BD D. ∠ABD=∠CBD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:一次函数 ![]() 的图象与反比例函数
的图象与反比例函数 ![]() 的图象交于M、N两点
的图象交于M、N两点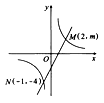
(1)求反比例函数和一次函数的关系式
(2)根据图象写出使反比例函数的值大于一次函数的值的x的取值范围
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市火车运货站现有甲种货物1530吨,乙种货物1150 吨,安排用一列货车将这批货物运往广州,这种货车可挂A、B两种不同规格的货厢50节.已知用一节A型货厢的运费是0.5万元,用一节B型货厢的运费是0.8万元.
(1)设运输这批货物的总运费y(万元),用A型货厢的节数为x(节),试写出y与x之间的函数关系式;
(2)已知甲种货物35吨和乙种货物15吨可装满一节A型货厢,甲种货物25吨和乙种货物35吨可装满一节B型货厢.按此要求安排A、B两种货厢的节数,有哪几种运输方案?请你设计出来;
(3)利用函数性质说明,在这些方案中,哪种方案总运费最少?最少运费是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BD、CE分别是边AC、AB上的中线,BD与CE相交于点O,点M、N分别是OB、OC的中点.
(1)求证:EN与DM互相平分;
(2)若AB=AC,判断四边形DEMN的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com