
【题目】已知AB是⊙O的直径,C为⊙O上一点,∠OAC=58°.

(Ⅰ)如图①,过点C作⊙O的切线,与BA的延长线交于点P,求∠P的大小;
(Ⅱ)如图②,P为AB上一点,CP延长线与⊙O交于点Q.若AQ=CQ,求∠APC的大小.
【答案】(I)∠P=26°;(II)∠APC=48°.
【解析】
(I)根据等腰三角形中有一底角为58度时,可得∠COA=64°,根据切线的性质得出∠OCP=90°,进而求得∠P的度数;
(II)先由(I)知∠AOC=64°,根据圆周角定理得∠Q=![]() ∠AOC=32°,根据等腰三角形的性质和三角形内角和定理得∠QAC=∠QCA=74°,最后由三角形外角的性质可得结论.
∠AOC=32°,根据等腰三角形的性质和三角形内角和定理得∠QAC=∠QCA=74°,最后由三角形外角的性质可得结论.
(I)如图①,

∵OA=OC,∠OAC=58°,
∴∠OCA=58°
∴∠COA=180°﹣2×58°=64°
∵PC是⊙O的切线,
∴∠OCP=90°,
∴∠P=90°﹣64°=26°;
(II)∵∠AOC=64°,
∴∠Q=![]() ∠AOC=32°,
∠AOC=32°,
∵AQ=CQ,
∴∠QAC=∠QCA=74°,
∵∠OCA=58°,
∴∠PCO=74°﹣58°=16°,
∵∠AOC=∠QCO+∠APC,
∴∠APC=64°﹣16°=48°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
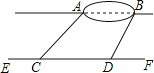
【题目】小明想测量湿地公园内某池塘两端A,B两点间的距离.他沿着与直线AB平行的道路EF行走,当行走到点C处,测得∠ACF=40°,再向前行走100米到点D处,测得∠BDF=52.44°,若直线AB与EF之间的距离为60米,求A,B两点的距离(结果精确到0.1)(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,sin52.44°≈0.79,cos52.44°≈0.61,tan52.44°≈1.30)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某篮球队5名场上队员的身高(单位:cm)是:183、187、190、200、210,现用一名身高为195cm的队员换下场上身高为210 cm的队员,与换人前相比,场上队员的身高 ( )
A.平均数变大,方差变大B.平均数变小,方差变小
C.平均数变大,方差变小D.平均数变小,方差变大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解初中学生每天在校体育活动的时间(单位:![]() ),随机调查了该校的部分初中学生.根据调查结果,绘制出如下的统计图1和图2.请根据相关信息,解答下列问题:
),随机调查了该校的部分初中学生.根据调查结果,绘制出如下的统计图1和图2.请根据相关信息,解答下列问题:
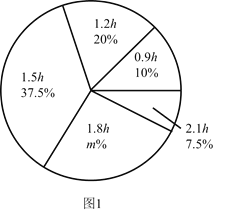
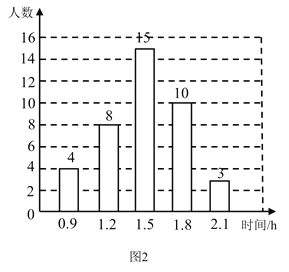
(Ⅰ)本次接受调查的初中学生人数为 ,图1中![]() 的值为 ;
的值为 ;
(Ⅱ)求统计的这组每天在校体育活动时间数据的平均数、众数和中位数;
(Ⅲ)根据统计的这组每天在校体育活动时间的样本数据,若该校共有1200名初中学生,估计该校每天在校体育活动时间大于![]() 的学生人数.
的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a≠0)经过点(1,1)和(﹣1,0).下列结论:①a+c=1;②b2﹣4ac≥0;③当a<0时,抛物线与x轴必有一个交点在点(1,0)的右侧;④抛物线的对称轴为x=﹣![]() .其中结论正确的个数有( )
.其中结论正确的个数有( )
A.4 个B.3 个C.2 个D.1 个
查看答案和解析>>
科目:初中数学 来源: 题型:
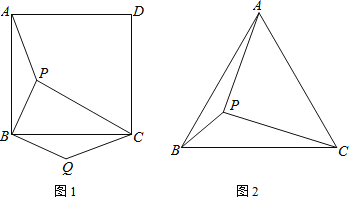
【题目】(1)如图1,点P是正方形ABCD内的一点,把△ABP绕点B顺时针方向旋转,使点A与点C重合,点P的对应点是Q.若PA=3,PB=2![]() ,PC=5,求∠BQC的度数.
,PC=5,求∠BQC的度数.
(2)点P是等边三角形ABC内的一点,若PA=12,PB=5,PC=13,求∠BPA的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课题:两个重叠的正多边形,其中的一个绕某一顶点旋转所形成的有关问题.
实验与论证:
设旋转角∠A1A0B1=α(α<∠A1A0A2),θ3、θ4、θ5、θ6所表示的角如图所示.
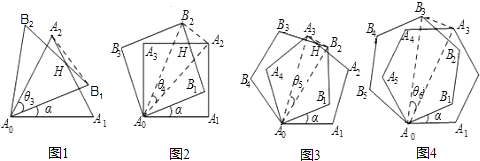
(1)用含α的式子表示角的度数:θ3= ,θ4= ,θ5= ;
(2)图1﹣图4中,连接A0H时,在不添加其他辅助线的情况下,是否存在与直线A0H垂直且被它平分的线段?若存在,请选择其中的一个图给出证明;若不存在,请说明理由;
归纳与猜想:
设正n边形A0A1A2…An﹣1与正n边形A0B1B2…Bn﹣1重合(其中,A1与B1重合),现将正多边形A0B1B2…Bn﹣1绕顶点A0逆时针旋转α(0°<α<![]() °);
°);
(3)设θn与上述“θ3、θ4、…”的意义一样,请直接写出θn的度数;
(4)试猜想在正n边形的情形下,是否存在与直线A0H垂直且被它平分的线段?若存在,请将这条线段用相应的顶点字母表示出来(不要求证明);若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解学生对世博礼仪的知晓程度,从全校1200名学生中随机抽取了50名学生进行测试.根据测试成绩(成绩取整数,满分为100分)作了统计分析,绘制成频数分布直方图(如图,其中部分数据缺失).又知90分以上(含90分)的人数比60~70分(含60分,不含70分)的人数的2倍还多3人.请你根据上述信息,解答下列问题:
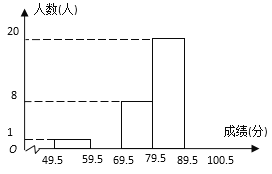
(1)该统计分析的样本是( )
A.1200名学生;
B.被抽取的50名学生;
C.被抽取的50名学生的问卷成绩;
D.50
(2)被测学生中,成绩不低于90分的有多少人?
(3)测试成绩的中位数所在的范围是 ;
(4)如果把测试成绩不低于80分记为优良,试估计该校有多少名学生对世博礼仪的知晓程度达到优良;
(5)学校准备从这50名学生中,以测试成绩不低于90分为标准,随机选3人义务宣传世博礼仪,若小杰的得分是93分,那么小杰被选上的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于点P(x,y),若点Q的坐标为(x,|x﹣y|),则称点Q为点P的“关联点”.
(1)请直接写出点(2,2)的“关联点”的坐标;
(2)如果点P在函数y=x﹣1的图象上,其“关联点”Q与点P重合,求点P的坐标;
(3)如果点M(m,n)的“关联点”N在函数y=x2的图象上,当0≤m≤2时,求线段MN的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com