
،¾جâؤ؟،؟ؤ³ذ£خھءثءث½âر§ةْ¶شتہ²©ہٌزاµؤضھد³ج¶ب£¬´سب«ذ£1200أûر§ةْضذثو»ْ³éب،ءث50أûر§ةْ½ّذذ²âتش£®¸ù¾ف²âتش³ة¼¨£¨³ة¼¨ب،صûت£¬آْ·ضخھ100·ض£©×÷ءثح³¼ئ·ضخِ£¬»وضئ³ةئµت·ض²¼ض±·½ح¼£¨بçح¼£¬ئنضذ²؟·ضت¾فب±ت§£©£®سضضھ90·ضزشةد£¨؛¬90·ض£©µؤبثت±ب60~70·ض£¨؛¬60·ض£¬²»؛¬70·ض£©µؤبثتµؤ2±¶»¹¶à3بث£®اëؤم¸ù¾فةدتِذإد¢£¬½â´ًدآءذختجâ£؛
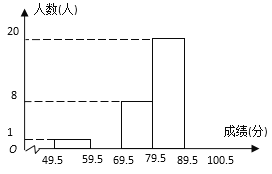
£¨1£©¸أح³¼ئ·ضخِµؤرù±¾تا£¨ £©
A.1200أûر§ةْ£»
B.±»³éب،µؤ50أûر§ةْ£»
C.±»³éب،µؤ50أûر§ةْµؤخت¾ي³ة¼¨£»
D.50
£¨2£©±»²âر§ةْضذ£¬³ة¼¨²»µحسع90·ضµؤسذ¶àةظبث£؟
£¨3£©²âتش³ة¼¨µؤضذخ»تثùشعµؤ·¶خ§تا £»
£¨4£©بç¹û°ر²âتش³ة¼¨²»µحسع80·ض¼اخھسإء¼£¬تش¹ہ¼ئ¸أذ£سذ¶àةظأûر§ةْ¶شتہ²©ہٌزاµؤضھد³ج¶ب´ïµ½سإء¼£»
£¨5£©ر§ذ£×¼±¸´سصâ50أûر§ةْضذ£¬زش²âتش³ة¼¨²»µحسع90·ضخھ±ê×¼£¬ثو»ْر،3بثزهخٌذû´«تہ²©ہٌزا£¬بôذ،½ـµؤµأ·ضتا93·ض£¬ؤاأ´ذ،½ـ±»ر،ةدµؤ¸إآتتا¶àةظ£؟
،¾´ً°¸،؟£¨1£©C£»£¨2£©15£»£¨3£©79.5،ھ89.5£»£¨4£©840£»£¨5£©![]()
،¾½âخِ،؟
£¨1£©¸ù¾فرù±¾µؤ¶¨زه£¬¸أح³¼ئ·ضخِµؤرù±¾تا±»³éب،µؤ50أûر§ةْµؤ²âتش³ة¼¨.
£¨2£©؟ةزشةè60،ھ،ھ70·ض£¨؛¬60·ض£¬²»؛¬70·ض£©µؤبثتخھ![]() بث£¬شٍ90·ضزشةد£¨؛¬90·ض£©µؤبثتخھ
بث£¬شٍ90·ضزشةد£¨؛¬90·ض£©µؤبثتخھ![]() £¬¸ù¾فجâؤ؟ضذµؤتء؟¹طدµءذ³ِز»شھز»´خ·½³ج½â´ً¼´؟ة.
£¬¸ù¾فجâؤ؟ضذµؤتء؟¹طدµءذ³ِز»شھز»´خ·½³ج½â´ً¼´؟ة.
£¨3£©¸ù¾فضذخ»تµؤ¶¨زهر°صزئنثùشعµؤ³ة¼¨اّ¼ن¼´؟ة.
£¨4£©¸ù¾فرù±¾اé؟ِ¼ئثم³ِ³ة¼¨سإء¼µؤر§ةْبثتثùص¼±بہ£¬شظ³ثزش¸أذ£ر§ةْ×ـبثت¼´؟ة.
£¨5£©سةµع£¨2£©خت؟ةضھ£¬90·ضزشةد£¨؛¬90·ض£©µؤبثتخھ15بث£¬°´صصر،بث¹وشٍذ،½ـسذ3´خ»ْ»ل£¬شٍ¸إآتخھ![]() £¬»¯¼ٍ¼´؟ة.
£¬»¯¼ٍ¼´؟ة.
£¨1£©C£»
£¨2£©½â£؛ةè60،ھ،ھ70·ض£¨؛¬60·ض£¬²»؛¬70·ض£©µؤبثتخھ![]() بث£¬شٍ90·ضزشةد£¨؛¬90·ض£©µؤبثتخھ
بث£¬شٍ90·ضزشةد£¨؛¬90·ض£©µؤبثتخھ![]() £¬
£¬
سةجâزâ؟ةµأ![]()
½âµأ![]() £¬
£¬
![]() .
.
ثùزش³ة¼¨²»µحسع90·ضµؤسذ15بث.
£¨3£©79.5،ھ89.5
£¨4£©![]() بث,¹ت¹ہ¼ئ¸أذ£سذ840أûر§ةْ¶شتہ²©ہٌزاµؤضھد³ج¶ب´ïµ½سإء¼.
بث,¹ت¹ہ¼ئ¸أذ£سذ840أûر§ةْ¶شتہ²©ہٌزاµؤضھد³ج¶ب´ïµ½سإء¼.
£¨5£©![]() .
.
¹تذ،½ـ±»ر،ةدµؤ¸إآتتا![]() .
.



| ؤ꼶 | ¸كضذ؟خ³ج | ؤ꼶 | ³ُضذ؟خ³ج |
| ¸كز» | ¸كز»أâ·ر؟خ³جحئ¼ِ£، | ³ُز» | ³ُز»أâ·ر؟خ³جحئ¼ِ£، |
| ¸ك¶ | ¸ك¶أâ·ر؟خ³جحئ¼ِ£، | ³ُ¶ | ³ُ¶أâ·ر؟خ³جحئ¼ِ£، |
| ¸كب | ¸كبأâ·ر؟خ³جحئ¼ِ£، | ³ُب | ³ُبأâ·ر؟خ³جحئ¼ِ£، |
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟ؤ³²؟أإخھذآµؤةْ²ْدكرذ·¢ءثز»؟î»ْئ÷بث£¬خھءثءث½âثüµؤ²ظ×÷¼¼ؤـاé؟ِ£¬شعدàح¬جُ¼دآسëبث¹¤²ظ×÷½ّذذءث³éرù¶ش±ب£®¹³جبçدآ£¬اë²¹³نحêصû£®
تص¼¯ت¾ف¶شح¬ز»¸ِةْ²ْ¶¯×÷£¬»ْئ÷بث؛حبث¹¤¸÷²ظ×÷20´خ£¬²âتش³ة¼¨£¨ت®·ضضئ£©بçدآ£؛
»ْئ÷بث | 8.0 | 8.1 | 8.1 | 8.1 | 8.2 | 8.2 | 8.3 | 8.4 | 8.4 | 9.0 |
9.0 | 9.0 | 9.1 | 9.1 | 9.4 | 9.5 | 9.5 | 9.5 | 9.5 | 9.6 | |
بث¹¤ | 6.1 | 6.2 | 6.6 | 7.2 | 7.2 | 7.5 | 8.0 | 8.2 | 8.3 | 8.5 |
9.1 | 9.6 | 9.8 | 9.9 | 9.9 | 9.9 | 10 | 10 | 10 | 10 |
صûہي،¢أèتِت¾ف°´بçدآ·ض¶خصûہي،¢أèتِصâء½×éرù±¾ت¾ف£؛
³ة¼¨x بثت ةْ²ْ·½ت½ | 6،ـx£¼7 | 7،ـx£¼8 | 8،ـx£¼9 | 9،ـx،ـ10 |
»ْئ÷بث | 0 | 0 | 9 | 11 |
بث¹¤ | ،، ،، | ،، ،، | ،، ،، |
£¨ثµأ÷£؛³ة¼¨شع9.0·ض¼°زشةدخھ²ظ×÷¼¼ؤـسإذم£¬8.0،«8.9·ضخھ²ظ×÷¼¼ؤـء¼؛أ£¬6.0،«7.9·ضخھ²ظ×÷¼¼ؤـ؛د¸ٌ£¬6.0·ضزشدآخھ²ظ×÷¼¼ؤـ²»؛د¸ٌ£©
·ضخِت¾فء½×éرù±¾ت¾فµؤئ½¾ùت،¢ضذخ»ت،¢ضعت؛ح·½²îبçدآ±يثùت¾£؛
ئ½¾ùت | ضذخ»ت | ضعت | ·½²î | |
»ْئ÷بث | 8.8 | ،،9.0،، | 9.5 | 0.333 |
بث¹¤ | 8.6 | ،،8.8،، | 10 | 1.868 |
µأ³ِ½لآغ
£¨1£©بç¹ûةْ²ْ³ِز»¸ِ²ْئ·£¬ذèزھحê³ةح¬رùµؤ²ظ×÷200´خ£¬¹ہ¼ئ»ْئ÷بثةْ²ْصâ¸ِ²ْئ·´ïµ½²ظ×÷¼¼ؤـسإذمµؤ´ختخھ،، ،،£»
£¨2£©اë½ل؛دت¾ف·ضخِ»ْئ÷بث؛حبث¹¤شع²ظ×÷¼¼ؤـ·½أو¸÷×شµؤسإتئ£؛،، ،،£®
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟زرضھABتا،رOµؤض±¾¶£¬Cخھ،رOةدز»µم£¬،دOAC£½58،م£®

£¨¢ٌ£©بçح¼¢ظ£¬¹µمC×÷،رOµؤاذدك£¬سëBAµؤرس³¤دك½»سعµمP£¬اَ،دPµؤ´َذ،£»
£¨¢ٍ£©بçح¼¢ع£¬PخھABةدز»µم£¬CPرس³¤دكسë،رO½»سعµمQ£®بôAQ£½CQ£¬اَ،دAPCµؤ´َذ،£®
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
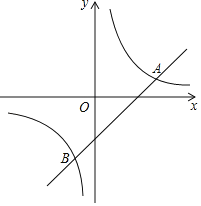
،¾جâؤ؟،؟بçح¼£¬شعئ½أوض±½ا×ّ±êدµxOyضذ£¬ض±دكy=x©پ2سëث«اْدكy=![]() (k،ظ0)دཻسعA£¬Bء½µم£¬ازµمAµؤ؛ل×ّ±êتا3£®
(k،ظ0)دཻسعA£¬Bء½µم£¬ازµمAµؤ؛ل×ّ±êتا3£®
(1)اَkµؤضµ£»
(2)¹µمP(0£¬n)×÷ض±دك£¬ت¹ض±دكسëxضلئ½ذذ£¬ض±دكسëض±دكy=x©پ2½»سعµمM£¬سëث«اْدكy=![]() (k،ظ0)½»سعµمN£¬بôµمMشعNسز±ك£¬اَnµؤب،ضµ·¶خ§£®
(k،ظ0)½»سعµمN£¬بôµمMشعNسز±ك£¬اَnµؤب،ضµ·¶خ§£®
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
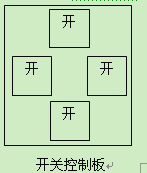
،¾جâؤ؟،؟ؤ³½جتزµؤ؟ھ¹ط؟طضئ°هةدسذثؤ¸ِحâذخحêب«دàح¬µؤ؟ھ¹ط£¬ئنضذء½¸ِ·ض±ً؟طضئA،¢Bء½
صµµçµئ£¬ءيء½¸ِ·ض±ً؟طضئC،¢Dء½¸ِµُةب.زرضھµçµئ،¢µُةب¾ùص³££¬از´¦سع²»¹¤×÷×´ج¬£¬؟ھ
¹طسëµçµئ،¢µçةبµؤ¶شس¦¹طدµخ´ضھ.
£¨1£©بôثؤ¸ِ؟ھ¹ط¾ùص³££¬شٍبخزâ°´دآز»¸ِ؟ھ¹ط£¬ص؛أز»صµµئءءµؤ¸إآتتا¶àةظ£؟
£¨2£©بôئنضذز»¸ِ؟طضئµçµئµؤ؟ھ¹ط»µءث£¬شٍبخزâ°´دآء½¸ِ؟ھ¹ط£¬ص؛أز»صµµئءء؛حز»¸ِةب×ھµؤ¸إآتتا¶àةظ£؟اëسأت÷×´ح¼·¨»ٍءذ±ي·¨¼سزشثµأ÷
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟بçح¼£¬BCخھش²Oض±¾¶£¬BFسëش²OدàاذسعµمB£¬CF½»ش²OسعA£¬EخھACةدز»µم£¬ت¹،دEBA£½،دFBA£¬بôEF£½6£¬tan،دF£½![]() £¬شٍCEµؤ³¤خھ_____£®
£¬شٍCEµؤ³¤خھ_____£®
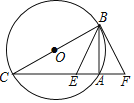
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟بçح¼£¬شعRt،÷ABCضذ£¬،دABC£½90،م£¬AB£½6£¬BC£½8£¬،دBAC£¬،دACBµؤئ½·ضدكدཻسعµمE£¬¹µمE×÷EF،خBC½»ACسعµمF£¬شٍEFµؤ³¤خھ£¨ £©
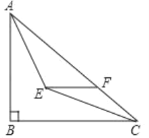
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟¼×،¢ززء½¸ِ¹¤³§ذè¼س¹¤ةْ²ْ 550 ج¨ؤ³ضض»ْئ÷£¬زرضھ¼×¹¤³§أ؟جى¼س¹¤ةْ²ْµؤ»ْئ÷ج¨تتازز¹¤³§أ؟جى¼س¹¤ ةْ²ْµؤ»ْئ÷ج¨تµؤ 1.5 ±¶£¬²¢از¼س¹¤ةْ²ْ 240 ج¨صâضض»ْئ÷¼×¹¤³§ذèزھµؤت±¼ن±بزز¹¤³§ذèزھµؤت±¼نةظ 4 جى
£¨1£©اَ¼×،¢ززء½¸ِ¹¤³§أ؟جى·ض±ً؟ةزش¼س¹¤ةْ²ْ¶àةظج¨صâضض»ْئ÷£؟
£¨2£©بô¼×¹¤³§أ؟جى¼س¹¤µؤةْ²ْ³ة±¾تا 3 حٍشھ£¬زز¹¤³§أ؟جى¼س¹¤ةْ²ْµؤ³ة±¾تا 2.4 حٍشھ£¬زھت¹µأ¼س¹¤ةْ ²ْصâإْ»ْئ÷µؤ×ـ³ة±¾²»µأ¸كسع 60 حٍشھ£¬ضءةظس¦¸أ°²إإ¼×¹¤³§ةْ²ْ¶àةظجى£؟
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟بçح¼£¬µم A µؤ×ّ±êتا£¨©پ2£¬0£©£¬µم B µؤ×ّ±êتا£¨0£¬6£©£¬C خھ OB µؤضذµم£¬½«،÷ABC بئµم B ؤوت±صëذ×ھ 90،م؛َµأµ½،÷A،نB،نC،ن£®بô·´±بہ؛¯ت y ![]() µؤح¼دَا،؛أ¾¹ A،نB µؤضذµم D£¬شٍk _________£®
µؤح¼دَا،؛أ¾¹ A،نB µؤضذµم D£¬شٍk _________£®
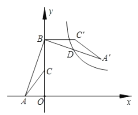
²é؟´´ً°¸؛ح½âخِ>>
¹ْ¼تر§ذ£سإر، - ء·د°²لءذ±ي - تشجâءذ±ي
؛±±ت،»¥ءھحّخ¥·¨؛ح²»ء¼ذإد¢¾ظ±¨ئ½ج¨ | حّةدسذ؛¦ذإد¢¾ظ±¨×¨اّ | µçذإص©ئ¾ظ±¨×¨اّ | ةوہْت·ذéخقض÷زهسذ؛¦ذإد¢¾ظ±¨×¨اّ | ةوئَاضب¨¾ظ±¨×¨اّ
خ¥·¨؛ح²»ء¼ذإد¢¾ظ±¨µç»°£؛027-86699610 ¾ظ±¨ستدن£؛58377363@163.com