
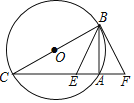
【题目】如图,BC为圆O直径,BF与圆O相切于点B,CF交圆O于A,E为AC上一点,使∠EBA=∠FBA,若EF=6,tan∠F=![]() ,则CE的长为_____.
,则CE的长为_____.
【答案】5![]()
【解析】
根据切线的性质和圆周角定理得出∠BAC=90°=∠BAF=∠FBC,根据全等三角形的判定得出△BAE≌△BAF,求出BE=BF,AE=AF,求出AE=AF=3,BF=BE=5,根据相似三角形的判定得出△FAB∽△FBC,根据相似三角形的性质得出比例式,求出FC长,即可得出答案.
解:∵BC为圆O直径,BF与圆O相切于点B,
∴∠BAC=90°=∠BAF=∠FBC,
在△BAE和△BAF中
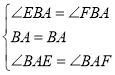
∴△BAE≌△BAF(ASA),
∴BE=BF,AE=AF,
∵EF=6,tan∠F=![]() =
=![]() ,
,
∴AE=AF=3,AB=5,
由勾股定理得:BF=![]() =
=![]() ,
,
∵∠BAF=∠FBC,∠F=∠F,
∴△FAB∽△FBC,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
解得:FC=![]() ,
,
∵AE=AF=3,
∴CE=![]() ﹣3﹣3=
﹣3﹣3=![]() ,
,
故答案为:5![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
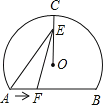
【题目】如图,点C是⊙O优弧ACB上的中点,弦AB=8cm,E为OC上任意一点,动点F从点A出发,以每秒1cm的速度沿AB方向向点B匀速运动,若y=AE2﹣EF2,则y与动点F的运动时间x(0≤x≤4)秒的函数关系式为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
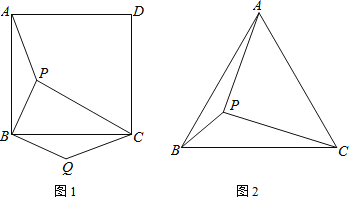
【题目】(1)如图1,点P是正方形ABCD内的一点,把△ABP绕点B顺时针方向旋转,使点A与点C重合,点P的对应点是Q.若PA=3,PB=2![]() ,PC=5,求∠BQC的度数.
,PC=5,求∠BQC的度数.
(2)点P是等边三角形ABC内的一点,若PA=12,PB=5,PC=13,求∠BPA的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
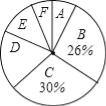
【题目】为了解某小区某月家庭用水量的情况,从该小区随机抽取部分家庭进行调查,以下是根据调查数据绘制的统计图表的一部分
分组 | 家庭用水量x/吨 | 家庭数/户 |
A | 0≤x≤4.0 | 4 |
B | 4.0<x≤6.5 | 13 |
C | 6.5<x≤9.0 | |
D | 9.0<x≤11.5 | |
E | 11.5<x≤14.0 | 6 |
F | x>4.0 | 3 |
根据以上信息,解答下列问题
(1)家庭用水量在4.0<x≤6.5范围内的家庭有 户,在6.5<x≤9.0范围内的家庭数占被调查家庭数的百分比是 %;
(2)本次调查的家庭数为 户,家庭用水量在9.0<x≤11.5范围内的家庭数占被调查家庭数的百分比是 %;
(3)家庭用水量的中位数落在 组;
(4)若该小区共有200户家庭,请估计该月用水量不超过9.0吨的家庭数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解学生对世博礼仪的知晓程度,从全校1200名学生中随机抽取了50名学生进行测试.根据测试成绩(成绩取整数,满分为100分)作了统计分析,绘制成频数分布直方图(如图,其中部分数据缺失).又知90分以上(含90分)的人数比60~70分(含60分,不含70分)的人数的2倍还多3人.请你根据上述信息,解答下列问题:
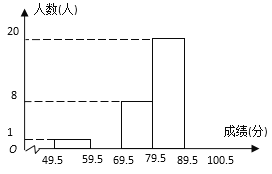
(1)该统计分析的样本是( )
A.1200名学生;
B.被抽取的50名学生;
C.被抽取的50名学生的问卷成绩;
D.50
(2)被测学生中,成绩不低于90分的有多少人?
(3)测试成绩的中位数所在的范围是 ;
(4)如果把测试成绩不低于80分记为优良,试估计该校有多少名学生对世博礼仪的知晓程度达到优良;
(5)学校准备从这50名学生中,以测试成绩不低于90分为标准,随机选3人义务宣传世博礼仪,若小杰的得分是93分,那么小杰被选上的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
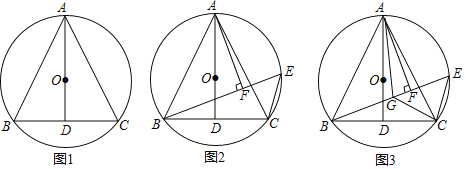
【题目】如图1,△ABC内接于圆O,连接AO,延长AO交BC于点D,AD⊥BC.
(1)求证:AB=AC;
(2)如图2,在圆O上取一点E,连接BE、CE,过点A作AF⊥BE于点F,求证:EF+CE=BF;
(3)如图3在(2)的条件下,在BE上取一点G,连接AG、CG,若![]() ∠AGB+∠ABC=90°,∠AGC=∠BGC,AG=6,BG=5,求EF的长.
∠AGB+∠ABC=90°,∠AGC=∠BGC,AG=6,BG=5,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
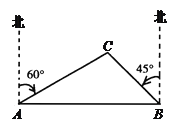
【题目】已知:如图,一艘渔船正在港口A的正东方向40海里的B处进行捕鱼作业,突然接到通知,要该船前往C岛运送一批物资到A港,已知C岛在A港的北偏东60°方向,且在B的北偏西45°方向.问该船从B处出发,以平均每小时20海里的速度行驶,需要多少时间才能把这批物资送到A港(精确到1小时)(该船在C岛停留半个小时)?(![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】科幻小说《实验室的故事》中,有这样一个情节,科学家把一种珍奇的植物分别放在不同温度的环境中,经过一段时间后,记录下这种植物高度的增长情况(如下表):
温度x/℃ | … | ﹣4 | ﹣2 | 0 | 2 | 4 | 6 | … |
植物每天高度的增长量y/mm | … | 41 | 49 | 49 | 41 | 25 | 1 | … |
由这些数据,科学家推测出植物每天高度的增长量y是温度x的二次函数,那么下列三个结论:
①该植物在0℃时,每天高度的增长量最大;
②该植物在﹣6℃时,每天高度的增长量能保持在25mm左右;
③该植物与大多数植物不同,6℃以上的环境下高度几乎不增长.
上述结论中,所有正确结论的序号是
A. ①②③ B. ①③ C. ①② D. ②③
查看答案和解析>>
科目:初中数学 来源: 题型:
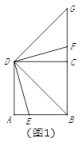
【题目】⑴如图1,![]() 是正方形
是正方形![]() 边
边![]() 上的一点,连接
上的一点,连接![]() ,将
,将![]() 绕着点
绕着点![]() 逆时针旋转90°,旋转后角的两边分别与射线
逆时针旋转90°,旋转后角的两边分别与射线![]() 交于点
交于点![]() 和点
和点![]() .
.
①线段![]() 和
和![]() 的数量关系是 ;
的数量关系是 ;
②写出线段![]() 和
和![]() 之间的数量关系.
之间的数量关系.
⑵当四边形![]() 为菱形,
为菱形,![]() ,点
,点![]() 是菱形
是菱形![]() 边
边![]() 所在直线上的一点,连接
所在直线上的一点,连接![]() ,将
,将![]() 绕着点
绕着点![]() 逆时针旋转120°,旋转后角的两边分别与射线
逆时针旋转120°,旋转后角的两边分别与射线![]() 交于点
交于点![]() 和点
和点![]() .
.
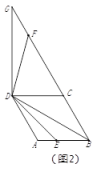
①如图2,点![]() 在线段上时,请探究线段
在线段上时,请探究线段![]() 和
和![]() 之间的数量关系,写出结论并给出证明;
之间的数量关系,写出结论并给出证明;
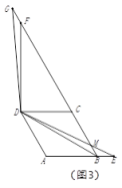
②如图3,点![]() 在线段
在线段![]() 的延长线上时,
的延长线上时,![]() 交射线
交射线![]() 于点
于点![]() ;若
;若 ![]() ,直接写出线段
,直接写出线段![]() 的长度.
的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com