
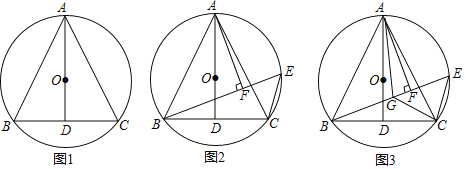
【题目】如图1,△ABC内接于圆O,连接AO,延长AO交BC于点D,AD⊥BC.
(1)求证:AB=AC;
(2)如图2,在圆O上取一点E,连接BE、CE,过点A作AF⊥BE于点F,求证:EF+CE=BF;
(3)如图3在(2)的条件下,在BE上取一点G,连接AG、CG,若![]() ∠AGB+∠ABC=90°,∠AGC=∠BGC,AG=6,BG=5,求EF的长.
∠AGB+∠ABC=90°,∠AGC=∠BGC,AG=6,BG=5,求EF的长.
【答案】(1)见解析;(2)见解析;(3)EF=![]() .
.
【解析】
(1)由垂径定理可得BD=CD,由垂直平分线的性质可得AB=AC;
(2)在BF上截取FH=EF,连接AE,由“SAS”可证△ABH≌△ACE,可得BH=CE,可得结论;
(3)延长CG交圆O于M,交AB于K,过点A作AP⊥CM于P,过点B作BN⊥CM于N,连接AE,通过等腰三角形的性质和相似三角形的性质,分别求出BF,CE的长,即可求EF的长.
证明:(1)∵AD⊥BC,AD过圆心O,
∴BD=CD,且AD⊥BC,
∴AB=AC;
(2)如图2,在BF上截取FH=EF,连接AE,AH,
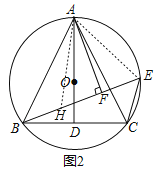
∵AF⊥EH,EF=FH,
∴AH=AE,
∴∠AHE=∠AEH,
∵AB=AC,
∴∠ABC=∠ACB,且∠ACB=∠AEH,
∴∠AEH=∠AHE=∠ABC=∠ACB,
∴∠BAC=∠HAE,
∴∠BAH=∠CAE,且AH=AE,AB=AC,
∴△ABH≌△ACE(SAS)
∴BH=CE,
∴BF=EF+CE;
(3)如图3,延长CG交⊙O于M,交AB于K,过点A作AP⊥CM于P,过点B作BN⊥CM于N,连接AE,AM,MB,
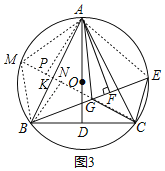
∵![]() ∠AGB+∠ABC=90°,
∠AGB+∠ABC=90°,
∴![]() ∠AGB=90°﹣∠ABC,
∠AGB=90°﹣∠ABC,
∴∠AGB=2∠BAC,
∵∠AGC=∠BGC,
∴∠BGM=∠AGM=![]() ∠AGB,
∠AGB,
∴∠BGM=∠AGM=∠BAC,且∠BAC=∠BMC,
∴∠BMG=∠BGM,
∴BM=BG=5,
∵∠AMC=∠ABC,∠AGM=∠BAC,
∴∠GAM=∠ACB,
∴∠AMG=∠MAG,
∴MG=AG=6,
∵BM=BG,BN⊥MG,
∴MN=NG=3,
∴BN=![]() =
=![]() =4,
=4,
∵∠BMG=∠AGM,
∴BM∥AG,
∴![]() ,
,
∵AP∥BN,
∴![]() ,
,
∴AP=![]() ,
,
∴PG=![]() ,
,
∴PN=PG﹣NG=![]() ,且
,且![]()
∴PK=![]() ,KN=
,KN=![]() ,
,
∴AK=![]() ,
,
BK=![]() ,
,
∴AB=AK+BK=![]() ,
,
∵AF2=AG2﹣GF2,AF2=AB2﹣BF2,
∴AG2﹣GF2=AB2﹣(5+GF)2,
∴GF=![]() ,
,
∴BF=![]() ,
,
∵MP=MG﹣PG=![]() ,
,
∴MK=![]() ,
,
∵∠AMC=∠ABC,∠MAB=∠BCM,
∴△MAK∽△BCK,
∴![]() ,
,
∴CK=![]() ,
,
∴GC﹣KC﹣KG=![]() ,
,
∵∠BMC=∠BEC,∠BGM=∠CGE,∠BGM=∠BMG,
∴∠CGE=∠CEG,
∴CG=CE=![]() ,
,
∵EF+CE=BF,
∴EF=BF﹣CE=![]() .
.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中(如图),已知抛物线y=ax2+4ax+c(a≠0)经过A(0,4),B(﹣3,1),顶点为C.
(1)求该抛物线的表达方式及点C的坐标;
(2)将(1)中求得的抛物线沿y轴向上平移m(m>0)个单位,所得新抛物线与y轴的交点记为点D.当△ACD时等腰三角形时,求点D的坐标;
(3)若点P在(1)中求得的抛物线的对称轴上,联结PO,将线段PO绕点P逆时针转90°得到线段PO′,若点O′恰好落在(1)中求得的抛物线上,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O的半径为2,AB为直径,CD为弦,AB与CD交于点M,将弧CD沿着CD翻折后,点A与圆心O重合,延长OA至P,使AP=OA,链接PC。

(1)求CD的长;
(2)求证:PC是⊙O的切线;
(3)点G为弧ADB的中点,在PC延长线上有一动点Q,连接QG交AB于点E,交弧BC于点F(F与B、C不重合)。问GEGF是否为定值?如果是,求出该定值;如果不是,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
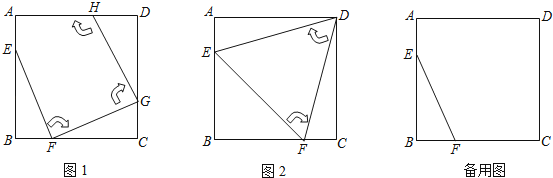
【题目】如图1,边长为4的正方形ABCD中,点E在AB边上(不与点A,B重合),点F在BC边上(不与点B、C重合).
第一次操作:将线段EF绕点F顺时针旋转,当点E落在正方形上时,记为点G;
第二次操作:将线段FG绕点G顺时针旋转,当点F落在正方形上时,记为点H;
依此操作下去…
(1)图2中的△EFD是经过两次操作后得到的,其形状为 ,求此时线段EF的长;
(2)若经过三次操作可得到四边形EFGH.
①请判断四边形EFGH的形状为 ,此时AE与BF的数量关系是 ;
②以①中的结论为前提,设AE的长为x,四边形EFGH的面积为y,求y与x的函数关系式及面积y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
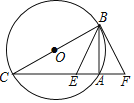
【题目】如图,BC为圆O直径,BF与圆O相切于点B,CF交圆O于A,E为AC上一点,使∠EBA=∠FBA,若EF=6,tan∠F=![]() ,则CE的长为_____.
,则CE的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
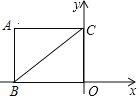
【题目】如图,平面直角坐标系中,矩形ABOC的边BO,CO分别在x轴,y轴上,A点的坐标为(﹣8,6),点P在矩形ABOC的内部,点E在BO边上,满足△PBE∽△CBO,当△APC是等腰三角形时,P点坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
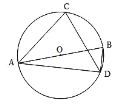
【题目】如图, AB 是⊙O 的直径,点 C 和点 D 是⊙O 上两点,连接 AC 、CD 、 BD ,若 CA= CD,∠ ACD = 80° ,则∠ CAB =______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】杂技团进行杂技表演,演员从跷跷板右端A处弹跳到人梯顶端椅子B处,其身体(看成一点)的路线是抛物线![]() 的一部分,如图
的一部分,如图

(1)求演员弹跳离地面的最大高度;
(2)已知人梯高BC=3.4米,在一次表演中,人梯到起跳点A的水平距离是4米,问这次表演是否成功?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个二次函数图象上部分点的横坐标![]() 与纵坐标
与纵坐标![]() 的对应值如表所示:
的对应值如表所示:
| … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | … |
| … | 0 | ﹣3 | ﹣4 | ﹣3 | 0 | … |
(1)求这个二次函数的表达式;
(2)在给定的平面直角坐标系中画出这个二次函数的图象;
(3)当![]() 时,直接写出
时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com