
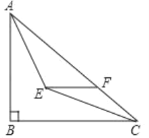
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=6,BC=8,∠BAC,∠ACB的平分线相交于点E,过点E作EF∥BC交AC于点F,则EF的长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
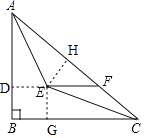
延长FE交AB于点D,作EG⊥BC、作EH⊥AC,由EF∥BC可证四边形BDEG是矩形,由角平分线可得ED=EH=EG、∠DAE=∠HAE,从而知四边形BDEG是正方形,再证△DAE≌△HAE、△CGE≌△CHE得AD=AH、CG=CH,设BD=BG=x,则AD=AH=6-x、CG=CH=8-x,由AC=10可得x=2,即BD=DE=2、AD=4,再证△ADF∽△ABC可得DF=![]() ,据此得出EF=DF-DE=
,据此得出EF=DF-DE=![]() .
.
解:如图,延长FE交AB于点D,作EG⊥BC于点G,作EH⊥AC于点H,
∵EF∥BC、∠ABC=90°,
∴FD⊥AB,
∵EG⊥BC,
∴四边形BDEG是矩形,
∵AE平分∠BAC、CE平分∠ACB,
∴ED=EH=EG,∠DAE=∠HAE,
∴四边形BDEG是正方形,
在△DAE和△HAE中,
∵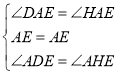 ,
,
∴△DAE≌△HAE(AAS),
∴AD=AH,
同理△CGE≌△CHE,
∴CG=CH,
设BD=BG=x,则AD=AH=6-x、CG=CH=8-x,
∵AC=![]() ,
,
∴6-x+8-x=10,
解得:x=2,
∴BD=DE=2,AD=4,
∵DF∥BC,
∴△ADF∽△ABC,
∴![]() ,即
,即![]() ,
,
解得:DF=![]() ,
,
则EF=DF-DE=![]() -2=
-2=![]() ,
,
故选C.


科目:初中数学 来源: 题型:
【题目】某篮球队5名场上队员的身高(单位:cm)是:183、187、190、200、210,现用一名身高为195cm的队员换下场上身高为210 cm的队员,与换人前相比,场上队员的身高 ( )
A.平均数变大,方差变大B.平均数变小,方差变小
C.平均数变大,方差变小D.平均数变小,方差变大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课题:两个重叠的正多边形,其中的一个绕某一顶点旋转所形成的有关问题.
实验与论证:
设旋转角∠A1A0B1=α(α<∠A1A0A2),θ3、θ4、θ5、θ6所表示的角如图所示.
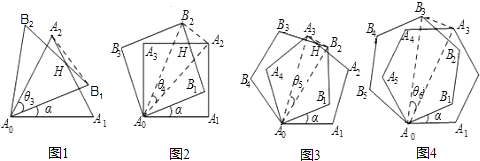
(1)用含α的式子表示角的度数:θ3= ,θ4= ,θ5= ;
(2)图1﹣图4中,连接A0H时,在不添加其他辅助线的情况下,是否存在与直线A0H垂直且被它平分的线段?若存在,请选择其中的一个图给出证明;若不存在,请说明理由;
归纳与猜想:
设正n边形A0A1A2…An﹣1与正n边形A0B1B2…Bn﹣1重合(其中,A1与B1重合),现将正多边形A0B1B2…Bn﹣1绕顶点A0逆时针旋转α(0°<α<![]() °);
°);
(3)设θn与上述“θ3、θ4、…”的意义一样,请直接写出θn的度数;
(4)试猜想在正n边形的情形下,是否存在与直线A0H垂直且被它平分的线段?若存在,请将这条线段用相应的顶点字母表示出来(不要求证明);若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解学生对世博礼仪的知晓程度,从全校1200名学生中随机抽取了50名学生进行测试.根据测试成绩(成绩取整数,满分为100分)作了统计分析,绘制成频数分布直方图(如图,其中部分数据缺失).又知90分以上(含90分)的人数比60~70分(含60分,不含70分)的人数的2倍还多3人.请你根据上述信息,解答下列问题:
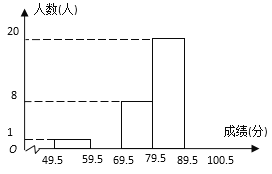
(1)该统计分析的样本是( )
A.1200名学生;
B.被抽取的50名学生;
C.被抽取的50名学生的问卷成绩;
D.50
(2)被测学生中,成绩不低于90分的有多少人?
(3)测试成绩的中位数所在的范围是 ;
(4)如果把测试成绩不低于80分记为优良,试估计该校有多少名学生对世博礼仪的知晓程度达到优良;
(5)学校准备从这50名学生中,以测试成绩不低于90分为标准,随机选3人义务宣传世博礼仪,若小杰的得分是93分,那么小杰被选上的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D在AB上,点E在AC延长线上,且BD=CE,连接DE交BC于点F,作DH⊥BC于点H,连接CD.若tan∠DFH=![]() ,S△BCD=18,则DE的长为_____.
,S△BCD=18,则DE的长为_____.
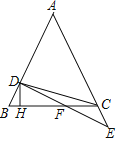
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,一艘渔船正在港口A的正东方向40海里的B处进行捕鱼作业,突然接到通知,要该船前往C岛运送一批物资到A港,已知C岛在A港的北偏东60°方向,且在B的北偏西45°方向.问该船从B处出发,以平均每小时20海里的速度行驶,需要多少时间才能把这批物资送到A港(精确到1小时)(该船在C岛停留半个小时)?(![]() ,
,![]() ,
,![]() )
)
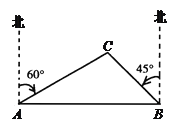
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形 ABCO 的一边 OA 在 x 轴上,![]() ,反比例函数
,反比例函数![]() 过菱形的顶点 C 和 AB 边上的中点E,则k的值为_______________.
过菱形的顶点 C 和 AB 边上的中点E,则k的值为_______________.
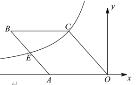
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于点P(x,y),若点Q的坐标为(x,|x﹣y|),则称点Q为点P的“关联点”.
(1)请直接写出点(2,2)的“关联点”的坐标;
(2)如果点P在函数y=x﹣1的图象上,其“关联点”Q与点P重合,求点P的坐标;
(3)如果点M(m,n)的“关联点”N在函数y=x2的图象上,当0≤m≤2时,求线段MN的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一名在校大学生利用“互联网+”自主创业,销售一种产品,这种产品的成本价10元/件,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于16元/件,市场调查发现,该产品每天的销售量![]() (件
(件![]() 与销售价
与销售价![]() (元/件)之间的函数关系如图所示.
(元/件)之间的函数关系如图所示.
(1)求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(2)求每天的销售利润W(元![]() 与销售价
与销售价![]() (元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?
(元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com