
【题目】甲、乙两个工厂需加工生产 550 台某种机器,已知甲工厂每天加工生产的机器台数是乙工厂每天加工 生产的机器台数的 1.5 倍,并且加工生产 240 台这种机器甲工厂需要的时间比乙工厂需要的时间少 4 天
(1)求甲、乙两个工厂每天分别可以加工生产多少台这种机器?
(2)若甲工厂每天加工的生产成本是 3 万元,乙工厂每天加工生产的成本是 2.4 万元,要使得加工生 产这批机器的总成本不得高于 60 万元,至少应该安排甲工厂生产多少天?
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】2019年全国两会于3月5日在人民大会堂开幕,某社区为了解居民对此次两会的关注程度,在全社区范围内随机抽取部分居民进行问卷调查,根据调查结果,把居民对两会的关注程度分成“淡薄”、“一般”、“较强”、“很强”四个层次,并绘制成如下不完整的统计图:
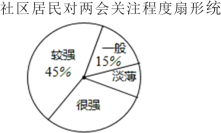
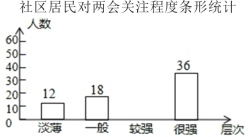
请结合图表中的信息,解答下列问题:
(1)此次调查一共随机抽取了_____名居民;
(2)请将条形统计图补充完整;
(3)扇形统计图中,“很强”所对应扇形圆心角的度数为_____;
(4)若该社区有1500人,则可以估计该社区居民对两会的关注程度为“淡薄”层次的约有 _____人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】榴莲上市的时候,某水果行以“线上”与“线下”相结合的方式一共销售了![]() 箱榴莲.已知“线上”销售的每箱利润为
箱榴莲.已知“线上”销售的每箱利润为![]() 元.“线下”销售的每箱利润
元.“线下”销售的每箱利润![]() (元)与销售量
(元)与销售量![]() (箱)
(箱)![]() 之间的函数关系如图中的线段
之间的函数关系如图中的线段![]() .
.
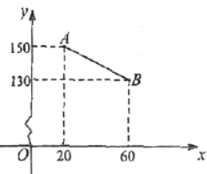
(1)求![]() 与
与![]() 之间的函数关系.
之间的函数关系.
(2)当“线下”的销售利润为![]() 元时,求
元时,求![]() 的值.
的值.
(3)实际“线下”销售时,每箱还要支出其它费用![]() 元
元![]() ,若“线上”与“线下”售完这
,若“线上”与“线下”售完这![]() 箱榴莲所获得的最大总利润为
箱榴莲所获得的最大总利润为![]() 元,求
元,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
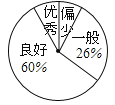
【题目】某校了解九年级学生近两个月“推荐书目”的阅读情况,随机抽取了该年级的部分学生,调查了他们每人“推荐书目”的阅读本数.设每名学生的阅读本数为n,并按以下规定分为四档:当n<3时,为“偏少”;当3≤n<5时,为“一般”;当5≤n<8时,为“良好”;当n≥8时,为“优秀”.将调查结果统计后绘制成不完整的统计图表:
阅读本数n(本) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
人数(名) | 1 | 2 | 6 | 7 | 12 | x | 7 | y | 1 |
请根据以上信息回答下列问题:
(1)分别求出统计表中的x、y的值;
(2)估计该校九年级400名学生中为“优秀”档次的人数;
(3)从被调查的“优秀”档次的学生中随机抽取2名学生介绍读书体会,请用列表或画树状图的方法求抽取的2名学生中有1名阅读本数为9的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B在反比例函数y=![]() (x>0)的图象上,点C,D在反比例函数y=
(x>0)的图象上,点C,D在反比例函数y=![]() (k>0)的图象上,AC∥BD∥y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为
(k>0)的图象上,AC∥BD∥y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为![]() ,则k的值为_____.
,则k的值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
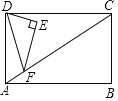
【题目】如图,在矩形ABCD中,AB=4,∠DCA=30°,点F是对角线AC上的一个动点,连接DF,以DF为斜边作∠DFE=30°的直角三角形DEF,使点E和点A位于DF两侧,点F从点A到点C的运动过程中,点E的运动路径长是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
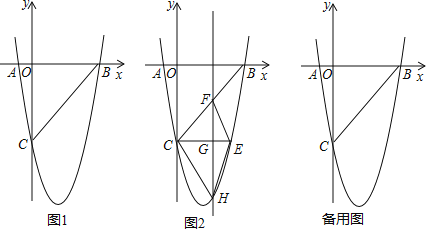
【题目】如图1,在平面直角坐标系中,已知抛物线y=ax2+bx﹣5与x轴交于A(﹣1,0),B(5,0)两点,与y轴交于点C.
(1)求抛物线的函数表达式;
(2)如图2,CE∥x轴与抛物线相交于点E,点H是直线CE下方抛物线上的动点,过点H且与y轴平行的直线与BC,CE分别相交于点F,G,试探究当点H运动到何处时,四边形CHEF的面积最大,求点H的坐标;
(3)若点K为抛物线的顶点,点M(4,m)是该抛物线上的一点,在x轴,y轴上分别找点P,Q,使四边形PQKM的周长最小,求出点P,Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解学生关注热点新闻的情况,“两会”期间,小明对班级同学一周内收看“两会”新闻的次数情况作了调查,调查结果统计如图所示(其中男生收看![]() 次的人数没有标出).
次的人数没有标出).
根据上述信息,解答下列各题:
 ×
×
(1)该班级女生人数是__________,女生收看“两会”新闻次数的中位数是________;
(2)对于某个群体,我们把一周内收看某热点新闻次数不低于![]() 次的人数占其所在群体总人数的百分比叫做该群体对某热点新闻的“关注指数”.如果该班级男生对“两会”新闻的“关注指数”比女生低
次的人数占其所在群体总人数的百分比叫做该群体对某热点新闻的“关注指数”.如果该班级男生对“两会”新闻的“关注指数”比女生低![]() ,试求该班级男生人数;
,试求该班级男生人数;
(3)为进一步分析该班级男、女生收看“两会”新闻次数的特点,小明给出了男生的部分统计量(如表).
统计量 | 平均数(次) | 中位数(次) | 众数(次) | 方差 | … |
该班级男生 |
|
|
|
| … |
根据你所学过的统计知识,适当计算女生的有关统计量,进而比较该班级男、女生收看“两会”新闻次数的波动大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一台实物投影仪,图2是它的示意图,折线O﹣A﹣B﹣C表示支架,支架的一部分O﹣A﹣B是固定的,另一部分BC是可旋转的,线段CD表示投影探头,OM表示水平桌面,AO⊥OM,垂足为点O,且AO=7cm,∠BAO=160°,BC∥OM,CD=8cm.
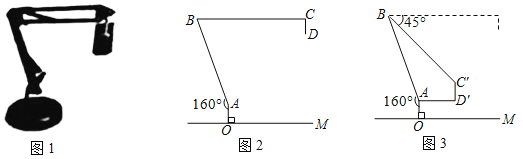
将图2中的BC绕点B向下旋转45°,使得BCD落在BC′D′的位置(如图3所示),此时C′D′⊥OM,AD′∥OM,AD′=16cm,求点B到水平桌面OM的距离,(参考数据:sin70°≈0.94,cos70°≈0.34,cot70°≈0.36,结果精确到1cm)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com