
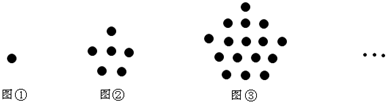
分析 通过观察图形得到:第①个图形中棋子的个数为1=1+5×0;第②个图形中棋子的个数为1+5=6;第③个图形中棋子的个数为1+5+10=1+5×(1+2)=16;…由此得出第n个图形中棋子的个数为1+5(1+2+…+n-1)=1+$\frac{5}{2}$n(n-1),然后把n=6代入计算即可.
解答 解:∵第①个图形中棋子的个数为1=1+5×0;
第②个图形中棋子的个数为1+5=6;
第③个图形中棋子的个数为1+5+10=1+5×(1+2)=16;
…
∴第n个图形中棋子的个数为1+5(1+2+…+n-1)=1+$\frac{5}{2}$n(n-1);
∴第⑥个图形中棋子的颗数为1+$\frac{5}{2}$×6×(6-1)=76.
故答案为:76.
点评 本题考查了图形的变化规律,通过从一些特殊的图形变化中发现不变的因素或按规律变化的因素,然后推广到一般情况.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
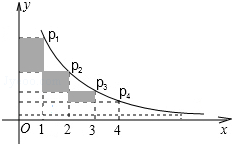 如图,在反比例函数y=$\frac{2}{x}$(x>0)的图象上,有点P1,P2,P3,…,P2010,它们的横坐标依次为1,2,3,…,2015.分别过这些点作
如图,在反比例函数y=$\frac{2}{x}$(x>0)的图象上,有点P1,P2,P3,…,P2010,它们的横坐标依次为1,2,3,…,2015.分别过这些点作查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,5),(-1,3).
在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,5),(-1,3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
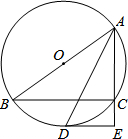 如图,AB是⊙O的直径,C为⊙O上一点,AD平分∠BAC交⊙O于点D,DE∥BC交AC延长线于点E.
如图,AB是⊙O的直径,C为⊙O上一点,AD平分∠BAC交⊙O于点D,DE∥BC交AC延长线于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com