
分析 (1)先计算判别式的值,再利用配方法得到△=4(t+2)2,利用非负数的性质可判断△>0,然后利用△=b2-4ac决定抛物线与x轴的交点个数判断此抛物线与x轴总有两个交点;
(2)利用求根公式法解方程x2-2(t+1)x-(2t+3)=0得到x1=2t+3,x2=-1,
①根据抛物线与x轴的交点问题可得到B(-1,0),A(2t+3,0),于是根据数轴上两点间的距离公式可得到AB=2t+4;
②由A、B的坐标得OB=1,OA=2t+3,根据题意得(2t+3-1)(1+1)=4,然后解方程即可.
解答 (1)证明:△=4(t+1)2+4(2t+3)
=4t2+16t+16
=4(t+2)2,
∵t>-1,
∴4(t+2)2>0,即△>0,
∴此抛物线与x轴总有两个交点;
(2)解:x2-2(t+1)x-(2t+3)=0,
△=4(t+2)2,
x=$\frac{2(t+1)±2(t+2)}{2}$,
所以x1=2t+3,x2=-1,
①B(-1,0),A(2t+3,0),
∵t>-1,
∴A、B两点之间的距离为AB=2t+3+1=2t+4;
②∵B(-1,0),A(2t+3,0),
∴OB=1,OA=2t+3,
∴(2t+3-1)(1+1)=4,解得t=0,
即t的值为0.
故答案为2t+4.
点评 本题考查了抛物线与x轴的交点问题:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程;△=b2-4ac决定抛物线与x轴的交点个数:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.解决本题的关键是利用公式法解一元二次方程.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
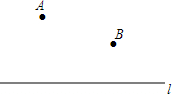 如图,点A,B为直线l外的两点,点P是直线l上的动点,当点P运动到何处时,PA与线段PB之差达到最大?请你在图上标出符合条件的点P的位置.
如图,点A,B为直线l外的两点,点P是直线l上的动点,当点P运动到何处时,PA与线段PB之差达到最大?请你在图上标出符合条件的点P的位置.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2<MN≤8 | B. | 2≤MN<8 | C. | 1<MN≤4 | D. | 1≤MN<4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com