
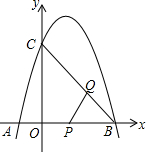
 ��ͼ����ƽ��ֱ������ϵ�У�������y=-x2+2x+3��x�ύ��A��B���㣨��A�ڵ�B��ࣩ����y�ύ��C�㣮����P�ӵ�B��������x�Ḻ������ÿ��1����λ���ٶ��˶�������P��PQ��BC������ΪQ���ٽ���PBQ�Ƶ�P����ʱ�뷽����ת90�㣮���P���˶�ʱ��Ϊt�룮
��ͼ����ƽ��ֱ������ϵ�У�������y=-x2+2x+3��x�ύ��A��B���㣨��A�ڵ�B��ࣩ����y�ύ��C�㣮����P�ӵ�B��������x�Ḻ������ÿ��1����λ���ٶ��˶�������P��PQ��BC������ΪQ���ٽ���PBQ�Ƶ�P����ʱ�뷽����ת90�㣮���P���˶�ʱ��Ϊt�룮���� �����֪����������֪�������������������Ľ������꣬ȷ��������PBQ�ǵ���ֱ�������Σ���ת90���
��1����t��ʾ����B�����꣬������κ�������ʽ����⼴�ɣ�
��2����t��ʾ��ת��ĵ�B�͵�Q�����꣬��϶��κ�������ʽ�г�����ʽ�������PQ��PB��BQ���������н���ķ�Χ��д����Χ���ɣ�
��� �⣺y=-x2+2x+3����x=0ʱ����ã�y=3������OC=3��
��y=0ʱ��0=-x2+2x+3����ã�x1=-1��x2=3�����ԣ�OA=1��OB=3��
���ԣ�A��-1��0����B��3��0����C��0��3��
��OC=OB=3����֪����OBC=45��
��PQ��BC��
���PBQ�ǵ���ֱ�������Σ�PQ=PB��
�˶�t���PB=t�����ù��ɶ�������BQ=PQ=$\frac{\sqrt{2}}{2}$t������PBQ�Ƶ�P����ʱ�뷽����ת90���PB��x�ᣬ����Q��QM��x�ᣬ����ΪM�������QPM=45�㣬
�ɹ��ɶ�������PM=QM=$\frac{1}{2}$t��
����P��3-t��0����Q��3-$\frac{3t}{2}$��$\frac{t}{2}$������B��3-t��t����
��1���ѵ�B��3-t��t���������y=-x2+2x+3�ã�t=-��3-t��2+2��3-t��+3����ã�t=3����t=0����ȥ��
���ԣ�t=3��
�ʴ�Ϊ��3
��2����PB��������y=-x2+2x+3�н��㣬���ڵ�B��3-t��t�������У���x=3-tʱ��y��t����3-t��-1������ã�-��3-t��2+2��3-t��+3��t��
��ã�4��t��3����t��0����ȥ��
��PQ��BQ��������y=-x2+2x+3��������ͬ���㣬����Q��3-$\frac{3t}{2}$��$\frac{t}{2}$�������У���x=3-$\frac{3t}{2}$ʱ��y��$\frac{t}{2}$����3-t��-1������ã���-��3-$\frac{3t}{2}$��2+2��3-$\frac{3t}{2}$��+3��$\frac{t}{2}$��
��ã�4��t��$\frac{22}{9}$����t��0����ȥ��
���ԣ���4��t��3ʱ��PB��PQ���������н��㣻��3��t��$\frac{22}{9}$ʱ��PQ��BQ���������н��㣬
����������
����ת��ġ�PBQ��������������������㣬��t��ȡֵ��Χ�ǣ�4��t��$\frac{22}{9}$
�ʴ�Ϊ��4��t��$\frac{22}{9}$
���� ������Ҫ�����߶��������ߵĽ��㣬������֪���������꣬��������г�����ʽ�ǽ���Ĺؼ������н�һԪ���β���ʽ���Ը��ݻ����κ�����ͼ����


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0�Ȳ�������Ҳ���Ǹ��� | B�� | ���ĸ�����-1 | ||
| C�� | û�о���ֵ��С���� | D�� | -2.1���Ƿ��� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��֪ʵ��a��b�������ϱ�ʾ�ĵ���ͼ������|a+b|+$\sqrt{{{��a-b+1��}^2}}$�Ľ��Ϊ��������
��֪ʵ��a��b�������ϱ�ʾ�ĵ���ͼ������|a+b|+$\sqrt{{{��a-b+1��}^2}}$�Ľ��Ϊ��������| A�� | 2b-1 | B�� | 2a+1 | C�� | -2a-1 | D�� | -2b+1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com