
 如图,△ABC的外角平分线CP和内角平分线BP相交于点P,若∠BPC=35°,则∠A=( )
如图,△ABC的外角平分线CP和内角平分线BP相交于点P,若∠BPC=35°,则∠A=( )| A. | 70° | B. | 80° | C. | 55° | D. | 65° |
分析 根据三角形的一个外角等于与它不相邻的两个内角的和可得∠ACD=∠A+∠ABC,∠PCD=∠P+∠PBC,根据角平分线的定义可得∠PBC=$\frac{1}{2}$∠ABC,∠PCD=$\frac{1}{2}$∠ACD,然后整理得到∠A=2∠P.
解答 解:由三角形的外角性质得,∠ACD=∠A+∠ABC,∠PCD=∠P+∠PBC,
∵∠ABC的平分线BP和外角∠ACD的平分线CP相交于点P,
∴∠PBC=$\frac{1}{2}$∠ABC,∠PCD=$\frac{1}{2}$∠ACD,
∴∠P+$\frac{1}{2}$∠ABC=$\frac{1}{2}$(∠A+∠ABC),
∴∠A=2∠P,
∵∠P=35°,
∴∠A=2×35°=70°.
故选:A.
点评 本题考查了三角形的内角和定理,三角形的一个外角等于与它不相邻的两个内角的和的性质,角平分线的定义,整体思想的利用是解题的关键.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
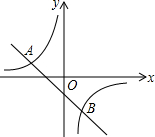 如图,一次函数y1=-x-1的图象与反比例函数y2=-$\frac{2}{x}$的图象交于A(-2,1),B(1,-2)两点,则使y2>y1的x的取值范围是( )
如图,一次函数y1=-x-1的图象与反比例函数y2=-$\frac{2}{x}$的图象交于A(-2,1),B(1,-2)两点,则使y2>y1的x的取值范围是( )| A. | -2<x<0或x>1 | B. | x<-2或x>1 | C. | x<-2或x>1 | D. | -2<x<1且x≠0 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
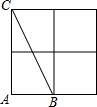 如图,△ABC的3个顶点分别在小正方形的顶点(格点)上,这样的三角形叫格点三角形,该图中与△ABC全等的不同格点三角形共有15个(△ABC除外).
如图,△ABC的3个顶点分别在小正方形的顶点(格点)上,这样的三角形叫格点三角形,该图中与△ABC全等的不同格点三角形共有15个(△ABC除外).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
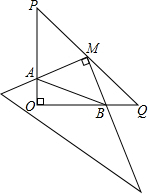 如图,在Rt△POQ中,OP=OQ=4,M是PQ中点,把一三角尺的直角顶点放在点M处,以M为旋转中心,旋转三角尺,三角尺的两直角边与△POQ的两直角边分别交于点A、B.连结AB,在旋转三角尺的过程中,△AOB的周长的最小值4+2$\sqrt{2}$.
如图,在Rt△POQ中,OP=OQ=4,M是PQ中点,把一三角尺的直角顶点放在点M处,以M为旋转中心,旋转三角尺,三角尺的两直角边与△POQ的两直角边分别交于点A、B.连结AB,在旋转三角尺的过程中,△AOB的周长的最小值4+2$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
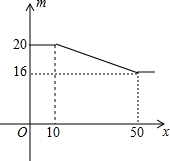 我市一家电子计算器专卖店的某种计算机每个进价13元,零售价20元,多买优惠;若顾客一次购买的数量x(个)与售出的单价m(元/个)的关系如图所示,售出的最低价为每个16元
我市一家电子计算器专卖店的某种计算机每个进价13元,零售价20元,多买优惠;若顾客一次购买的数量x(个)与售出的单价m(元/个)的关系如图所示,售出的最低价为每个16元查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com