
分析 (1)设原销售电价为每千瓦时x元,平段用电费用+谷段用电费用=42.73元,即:40(原售电价+0.03元)+60(原售电价-0.25元)=42.73元,据此列方程求解;
(2)求出原售电价,已知2月份的用电量,就比较容易求出:如不使用分时电价结算,2月份小明家将支付电费.从而算出多支付的电费数.
解答 解:(1)设原销售电价为每千瓦时x元,
根据题意得:40×(x+0.03)+60×(x-0.25)=42.73
解得:x=0.5653,
∴当x=0.5653时,x+0.03=0.5953,
x-0.25=0.3153.
答:小明家该月支付平段电价为每千瓦时0.5953元、谷段电价每千瓦时0.3153元;
(2)100×0.5653-42.73=13.8(元).
答:如不使用分时电价结算,小明家2月份将多支付13.8元.
点评 本题考查了一元一次方程的应用,解答本题的关键是读懂题意,设出未知数,正确找出题目中的相等关系,列方程求解.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
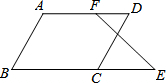 已知:如图,AB∥CD.∠A+∠DCE=180°,求证:∠E=∠DFE.
已知:如图,AB∥CD.∠A+∠DCE=180°,求证:∠E=∠DFE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 15×107千米 | B. | 1.5千米 | C. | 1.5×108千米 | D. | 0.15×107千米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com