
杂技团进行杂技表演,演员从跷跷板右端A处弹跳到人梯顶端椅子B处,其身体(看成一点)的路线是抛物线 的一部分,如图.
的一部分,如图.
(1)求演员弹跳离地面的最大高度;
(2)已知人梯高BC=3.4米,在一次表演中,人梯到起跳点A的水平距离是4米,问这次表演是否成功?请说明理由.

 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源:2014-2015学年浙江省九年级上学期第二次月考数学试卷(解析版) 题型:填空题
用长为8米的铝合金制成如图所示的窗框,若设窗框的宽为x 米,窗户的透光面积为S平方米,
则S关于x的函数关系式 .

查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省金华市新世纪学校九年级上学期期中测试数学试卷(解析版) 题型:解答题
如图,在直角坐标系中,以点A( ,0 )为圆心,以2
,0 )为圆心,以2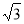 为半径的圆与x轴相交于点B、C,与y轴相交于点D、E
为半径的圆与x轴相交于点B、C,与y轴相交于点D、E

(1)若抛物线 经过C、D两点,求抛物线的表达式,并判断点B是否在该抛物线上
经过C、D两点,求抛物线的表达式,并判断点B是否在该抛物线上
(2)在(1)中的抛物线的对称轴上求一点P,使得△PBD的周长最小
(3)设Q为(1)中的抛物线对称轴上的一点,在抛物线上是否存在这样的点M,使得四边形BCQM是平行四边形,若存在,求出点M的坐标;若不存在,说明理由
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省金华市新世纪学校八年级上学期期中数学试卷(解析版) 题型:选择题
如图,△ABC中,∠C=90°,AB的中垂线DE交AB于E,交BC于D,若AB=10,AC=6,则△ACD的周长为( )

A.14 B.16 C.18 D.20
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省金华市新世纪学校八年级上学期期中数学试卷(解析版) 题型:解答题
如图,已知在△ABC中,∠B=90°,AB=8cm,BC=6cm,点P从点A开始沿△ABC的边做逆时针运动,且速度为每秒1cm;点Q从点B开始沿△ABC的边做逆时针运动,且速度为每秒2cm,他们同时出发,设运动时间为t秒.

(1)出发2秒后,P,Q两点间的距离为多少cm?
(2)在运动过程中,△PQB能形成等腰三角形吗?若能,请求出几秒后第一次形成等腰三角形;若不能,则说明理由.
(3)出发几秒后,线段PQ第一次把△ABC的周长分成相等两部分?
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省绍兴市六校九年级上学期第一次联考数学试卷(解析版) 题型:选择题
若M( ,y1)、N(
,y1)、N( ,y2)、P(
,y2)、P( ,y3)三点都在函数
,y3)三点都在函数 (
( )的图象上,则yl、y2、y3的大小关系是( )
)的图象上,则yl、y2、y3的大小关系是( )
A.y2>y3>y1 B.y2>y1>y3 C.y3>y1>y2 D.y3>y2>y1
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省绍兴市六校九年级上学期第一次联考数学试卷(解析版) 题型:解答题
如图,反比例函数 的图象与一次函数
的图象与一次函数 的图象交于点A(m,2),点B(-2, n ),一次函数图象与y轴的交点为C.求△AOC的面积。
的图象交于点A(m,2),点B(-2, n ),一次函数图象与y轴的交点为C.求△AOC的面积。

查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省温州市塘下学区七年级上学期期中联考数学试卷(解析版) 题型:填空题
如果规定符号“※”的意义是: ※
※ =
= ,则5※【2※(-2)】的值等于 .
,则5※【2※(-2)】的值等于 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com