
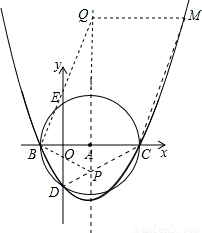
如图,在直角坐标系中,以点A( ,0 )为圆心,以2
,0 )为圆心,以2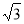 为半径的圆与x轴相交于点B、C,与y轴相交于点D、E
为半径的圆与x轴相交于点B、C,与y轴相交于点D、E

(1)若抛物线 经过C、D两点,求抛物线的表达式,并判断点B是否在该抛物线上
经过C、D两点,求抛物线的表达式,并判断点B是否在该抛物线上
(2)在(1)中的抛物线的对称轴上求一点P,使得△PBD的周长最小
(3)设Q为(1)中的抛物线对称轴上的一点,在抛物线上是否存在这样的点M,使得四边形BCQM是平行四边形,若存在,求出点M的坐标;若不存在,说明理由
(1) y=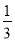 x2-
x2-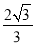 x-3,点B(-
x-3,点B(-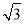 ,0)在抛物线上;
,0)在抛物线上;
(2)(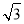 ,-2);
,-2);
(3)存在,M(-3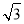 ,12)或(5
,12)或(5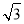 ,12)或(
,12)或(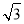 ,-4).
,-4).
【解析】
试题分析:(1)根据题意A(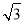 ,0),得出B(-
,0),得出B(-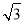 ,0)连接AD,在Rt△AOD中,可求OD,即D(0,-3),把C,D两点坐标代入抛物线y=
,0)连接AD,在Rt△AOD中,可求OD,即D(0,-3),把C,D两点坐标代入抛物线y=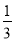 x2+bx+c,可求抛物线解析式;
x2+bx+c,可求抛物线解析式;
(2)由(1)知,点B关于抛物线对称轴的对称点为点C,连接CD,交抛物线对称轴于P点,P点即为所求,先求直线CD的解析式,已知P点横坐标x=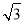 ,代入直线CD的解析式即可求P;
,代入直线CD的解析式即可求P;
(3)利用BC=4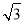 ,Q点横坐标是
,Q点横坐标是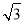 ,当M在Q点左边,则M点横坐标为
,当M在Q点左边,则M点横坐标为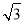 -4
-4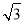 =-3
=-3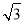 ,代入抛物线解析式可求M点坐标,进而利用当M在Q点右边求出M点坐标,.
,代入抛物线解析式可求M点坐标,进而利用当M在Q点右边求出M点坐标,.
试题解析:(1)如图:
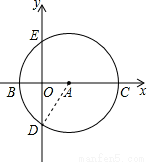
∵OA=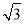 ,AB=AC=2
,AB=AC=2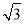 ,
,
∴B(-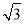 ,0),C(3
,0),C(3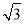 ,0),
,0),
在Rt△AOD中,AD=2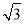 ,OA=
,OA=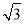 ,
,
∴OD=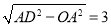
∴D的坐标为:(0,-3),
又D,C两点在抛物线上,
则
解得:
则抛物线的解析式为:y=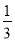 x2-
x2-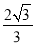 x-3,
x-3,
当x=-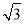 时,y=0,
时,y=0,
故点B(-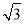 ,0)在抛物线上;
,0)在抛物线上;
(2)如图:
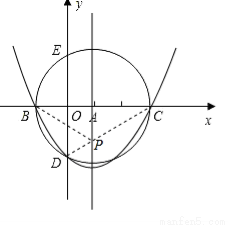
∵y=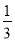 x2-
x2-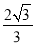 x-3=
x-3=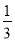 (x-
(x-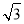 )2-4,
)2-4,
∴抛物线y=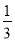 x2-
x2-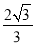 x-3的对称轴方程为:x=
x-3的对称轴方程为:x=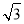 ,
,
在抛物线的对称轴上存在点P,使△PBD的周长最小.
∵BD的长为定值,
∴要使△PBD周长最小只需PB+PD最小.
连结DC,则DC与对称轴的交点即为使△PBD周长最小的点.
设直线DC的解析式为y=mx+n.
由
解得:
∴直线DC的解析式为:y=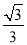 x-3,
x-3,
由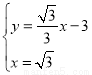
解得: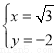
故点P的坐标为:(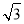 ,-2);
,-2);
(3)存在,
如图:
设Q(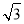 ,t)为抛物线对称轴x=
,t)为抛物线对称轴x=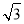 上一点,M在抛物线上要使四边形BCQM为平行四边形,
上一点,M在抛物线上要使四边形BCQM为平行四边形,
则BC∥QM且BC=QM,点M在对称轴的左侧.
于是,过点Q作直线L∥BC与抛物线交于点M(xm,t),
由BC=QM得QM=4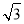 从而xm=-3
从而xm=-3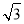 ,
,
故t=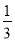 x2-
x2-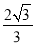 x-3
x-3
解得:t=12,
故在抛物线上存在点M(-3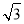 ,12),使得四边形BCQM为平行四边形;
,12),使得四边形BCQM为平行四边形;
故当M在Q点右边MQ=4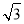 ,则M点横坐标为:5
,则M点横坐标为:5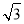 ,可得纵坐标为:12,
,可得纵坐标为:12,
另外:M在抛物线的顶点上也可以构造平行四边形,此时顶点坐标为:(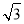 ,-4),
,-4),
故在抛物线上存在点M(-3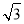 ,12)或(5
,12)或(5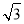 ,12)或(
,12)或(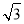 ,-4),使得四边形BCQM为平行四边形.
,-4),使得四边形BCQM为平行四边形.
考点:二次函数综合题.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案科目:初中数学 来源:2014-2015学年浙江省杭州市萧山地区九年级上学期期中考试数学试卷(解析版) 题型:填空题
将y=2x2-12x-12变为y=a(x-m)2+n的形式,则m·n=
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省金华市新世纪学校九年级上学期期中测试数学试卷(解析版) 题型:选择题
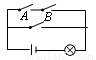
如图所示,电路图上有A、B、C三个开关和一个小灯泡,闭合开关C或者同时闭合开关A、B,都可使小灯泡发光.现在任意闭合其中一个开关,则小灯泡发光的概率等于( )
(A)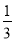 (B)
(B)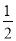 (C)
(C)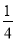 (D)
(D)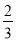
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省金华市新世纪学校八年级上学期期中数学试卷(解析版) 题型:选择题
如图,在△ABC中,∠A=35°,∠C=45°,则与∠ABC相邻的外角的度数是( )

A.80° B.45° C.35° D.120°
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省金华市新世纪学校八年级上学期期中数学试卷(解析版) 题型:解答题
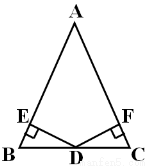
已知:如图,D是△ABC的BC边上的中点,DE⊥AB,DF⊥AC,垂足分别为E,F,且DE=DF.求证: △ABC是等腰三角形.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省绍兴市六校九年级上学期第一次联考数学试卷(解析版) 题型:解答题
杂技团进行杂技表演,演员从跷跷板右端A处弹跳到人梯顶端椅子B处,其身体(看成一点)的路线是抛物线 的一部分,如图.
的一部分,如图.
(1)求演员弹跳离地面的最大高度;
(2)已知人梯高BC=3.4米,在一次表演中,人梯到起跳点A的水平距离是4米,问这次表演是否成功?请说明理由.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省八年级上学期期中考试数学试卷(解析版) 题型:选择题
如图,D和E分别是 的边BC和AC上的点,若AB=AC,AD=AE,则下列说法正确的是( )
的边BC和AC上的点,若AB=AC,AD=AE,则下列说法正确的是( )

A.当 为定值时,
为定值时,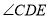 为定值
为定值
B.当 为定值时,
为定值时,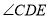 为定值
为定值
C.当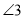 为定值时,
为定值时,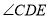 为定值
为定值
D.当 为定值时,
为定值时,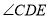 为定值
为定值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com