练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    将y=2x2－12x－12变为y=a（x－m）2+n的形式，则m·n=

     

    -90

    【解析】

    试题分析：∵y=2x2﹣12x﹣12=2（x2﹣6x+9）﹣18﹣12=2（x﹣3）2﹣30，

    ∴m=3，n=﹣30，

    ∴m•n=﹣90

    考点: 二次函数的三种形式

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2014-2015学年浙江省杭州地区八年级上学期期中质量检测数学试卷（解析版） 题型：选择题

    如图，在△ABC中，∠BCA＝90º，CA＝CB，AD为BC边上的中线，CG⊥AD于G，交AB于F，过点B作B C的垂线交C G于E．现有下列结论：①△ADC≌△CEB；②AB＝CE；③∠ADC＝∠BDF； ④F为EG中点．其中结论正确的个数为（ ）

    A．1 B．2 C．3 D．4

     

    查看答案和解析>>

    科目：初中数学 来源：2014-2015学年浙江省杭州市萧山区高桥教育九年级上学期第二次检测数学试卷（解析版） 题型：选择题

    根据下列表格中二次函数y＝Ax2＋Bx＋C的自变量与函数值的对应值，判断方程Ax2＋B x＋C=0（A≠0）的一个解的范围是（ ）

     

    6.17

    6.18

    6.19

    6.20

    y＝Ax2＋B x＋C

     

    A．6＜x＜6.17 B．6.17＜x＜6.18

    C．6.18＜x＜6.19 D．6.19＜x＜6.20

     

    查看答案和解析>>

    科目：初中数学 来源：2014-2015学年浙江省杭州市萧山区高桥教育九年级上学期第二次检测数学试卷（解析版） 题型：解答题

    （本小题满分12分）对于二次函数y=x²－3x+2和一次函数y=－2x+4，把y=t（x²－3x+2）+（1－t）（－2x+4）称为这两个函数的“再生二次函数”，其中t是不为零的实数，其图象记作抛物线L.现有点A（2，0）和抛物线L上的点B（－1，n），请完成下列任务：

    【尝试】

    （1）当t=2时，抛物线y=t（x²－3x+2）+（1－t）（－2x+4）的顶点坐标为 ；

    （2）判断点A是否在抛物线L上；

    （3）求n的值；

    【发现】

    通过（2）和（3）的演算可知，对于t取任何不为零的实数，抛物线L总过定点，坐标为 .

    【应用】

    二次函数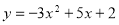是二次函数y=x²－3x+2和一次函数y=－2x+4的一个“再生二次函数”吗？如果是，求出t的值；如果不是，说明理由

     

    查看答案和解析>>

    科目：初中数学 来源：2014-2015学年浙江省杭州市萧山地区九年级上学期期中考试数学试卷（解析版） 题型：选择题

    时钟分针的长5cm，经过45分钟，它的针尖转过的弧长是（ ）

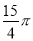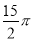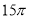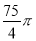    A. cm B. cm C. cm D. cm

     

    查看答案和解析>>

    科目：初中数学 来源：2014-2015学年浙江省杭州市萧山地区九年级上学期期中考试数学试卷（解析版） 题型：解答题

    (本小题满分10分 ）在端午节前夕三位同学到某超市调研一种进价为2元的粽子的售销情况，请跟据小丽提供的信息，解答小华和小明提出的问题

    小丽：每个定价3元，每天能卖出500个，而且，这种粽子每上涨0.1元，其售销量将减小10个

    小华：照你所说，如果实现每天800元的售销利润，那该如何定价？莫忘了物价局规定售价不能超过进价的240%哟

    小明：800元售销利润是不是最多的呢？如果不是，那该如何定价，才会使每天的利润最大？．

    （1）小华的问题解答：

    （2）小明的问题解答：

     

    查看答案和解析>>

    科目：初中数学 来源：2014-2015学年浙江省杭州市萧山地区九年级上学期期中考试数学试卷（解析版） 题型：填空题

    在在平面直角坐标系中，O是原点，A是x轴上的点，将射线OA绕点O旋转，使点A与双曲线y=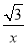上的点B重合，若点B的纵坐标是1，则点A的坐标是

     

     

    查看答案和解析>>

    科目：初中数学 来源：2014-2015学年浙江省九年级上学期第二次月考数学试卷（解析版） 题型：填空题

    用长为8米的铝合金制成如图所示的窗框，若设窗框的宽为x 米，窗户的透光面积为S平方米，

    则S关于x的函数关系式 ．

     

     

    查看答案和解析>>

    科目：初中数学 来源：2014-2015学年浙江省金华市新世纪学校九年级上学期期中测试数学试卷（解析版） 题型：解答题

    如图，在直角坐标系中，以点A（，0 ）为圆心，以2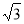为半径的圆与x轴相交于点B、C，与y轴相交于点D、E

    （1）若抛物线经过C、D两点，求抛物线的表达式，并判断点B是否在该抛物线上

    （2）在（1）中的抛物线的对称轴上求一点P，使得△PBD的周长最小

    （3）设Q为（1）中的抛物线对称轴上的一点，在抛物线上是否存在这样的点M，使得四边形BCQM是平行四边形，若存在，求出点M的坐标；若不存在，说明理由

     

    查看答案和解析>>

    同步练习册答案