
【题目】已知在矩形ABCD中,∠ADC的平分线DE与BC边所在的直线交于点E,点P是线段DE上一定点(其中EP<PD)
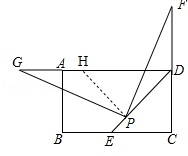
(1)如图1,若点F在CD边上(不与D重合),将∠DPF绕点P逆时针旋转90°后,角的两边PD、PF分别交射线DA于点H、G.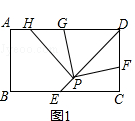
①求证:PG=PF; ②探究:DF、DG、DP之间有怎样的数量关系,并证明你的结论.
(2)拓展:如图2,若点F在CD的延长线上(不与D重合),过点P作PG⊥PF,交射线DA于点G,你认为(1)中DF、DG、DP之间的数量关系是否仍然成立?若成立,给出证明;若不成立,请写出它们所满足的数量关系式,并说明理由.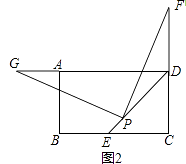
【答案】
(1)
解:①∵∠GPF=∠HPD=90°,∠ADC=90°,
∴∠GPH=∠FPD,
∵DE平分∠ADC,
∴∠PDF=∠ADP=45°,
∴△HPD为等腰直角三角形,
∴∠DHP=∠PDF=45°,
在△HPG和△DPF中,
∵ 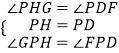 ,
,
∴△HPG≌△DPF(ASA),
∴PG=PF;
②结论:DG+DF= ![]() DP,
DP,
由①知,△HPD为等腰直角三角形,△HPG≌△DPF,
∴HD= ![]() DP,HG=DF,
DP,HG=DF,
∴HD=HG+DG=DF+DG,
∴DG+DF= ![]() DP
DP
(2)
解:不成立,数量关系式应为:DG﹣DF= ![]() DP,
DP,
如图,过点P作PH⊥PD交射线DA于点H,
∵PF⊥PG,
∴∠GPF=∠HPD=90°,
∴∠GPH=∠FPD,
∵DE平分∠ADC,且在矩形ABCD中,∠ADC=90°,
∴∠HDP=∠EDC=45°,得到△HPD为等腰直角三角形,
∴∠DHP=∠EDC=45°,且PH=PD,HD= ![]() DP,
DP,
∴∠GHP=∠FDP=180°﹣45°=135°,
在△HPG和△DPF中,
∵ 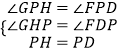
∴△HPG≌△DPF,
∴HG=DF,
∴DH=DG﹣HG=DG﹣DF,
∴DG﹣DF= ![]() DP
DP
【解析】(1)①若证PG=PF,可证△HPG≌△DPF,已知∠DPH=∠HPG,由旋转可知∠GPF=∠HPD=90°及DE平分∠ADC得△HPD为等腰直角三角形,即∠DHP=∠PDF=45°、PD=PH,即可得证;②由△HPD为等腰直角三角形,△HPG≌△DPF知HD= ![]() DP,HG=DF,根据DG+DF=DG+GH=DH即可得;(2)过点P作PH⊥PD交射线DA于点H,先证△HPD为等腰直角三角形可得PH=PD,HD=
DP,HG=DF,根据DG+DF=DG+GH=DH即可得;(2)过点P作PH⊥PD交射线DA于点H,先证△HPD为等腰直角三角形可得PH=PD,HD= ![]() DP,再证△HPG≌△DPF可得HG=DF,根据DH=DG﹣HG=DG﹣DF可得DG﹣DF=
DP,再证△HPG≌△DPF可得HG=DF,根据DH=DG﹣HG=DG﹣DF可得DG﹣DF= ![]() DP.
DP.


科目:初中数学 来源: 题型:
【题目】随着人民生活水平的提高,购买老年代步车的人越来越多.这些老年代步车却成为交通安全的一大隐患.针对这种现象,某校数学兴趣小组在《老年代步车现象的调查报告》中就“你认为对老年代步车最有效的管理措施”随机对某社区部分居民进行了问卷调查,其中调查问卷设置以下选项(只选一项): A:加强交通法规学习;
B:实行牌照管理;
C:加大交通违法处罚力度;
D:纳入机动车管理;
E:分时间分路段限行
调查数据的部分统计结果如下表:
管理措施 | 回答人数 | 百分比 |
A | 25 | 5% |
B | 100 | m |
C | 75 | 15% |
D | n | 35% |
E | 125 | 25% |
合计 | a | 100% |
(1)根据上述统计表中的数据可得m= , n= , a=;
(2)在答题卡中,补全条形统计图; 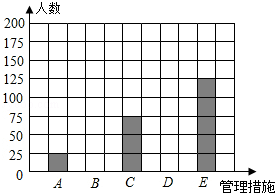
(3)该社区有居民2600人,根据上述调查结果,请你估计选择“D:纳入机动车管理”的居民约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“低碳环保,绿色出行”的概念得到广大群众的接受,越来越多的人喜欢选择骑自行车作为出行工具.小军和爸爸同时骑车去图书馆,爸爸先以150米/分的速度骑行一段时间,休息了5分钟,再以m米/分的速度到达图书馆.小军始终以同一速度骑行,两人骑行的路程为y(米)与时间x(分钟)的关系如图.请结合图象,解答下列问题:
(1)填空:a=________;b=________;m=________.
(2)若小军的速度是 120 米/分,求小军第二次与爸爸相遇时距图书馆的距离.
(3)在(2)的条件下,爸爸自第二次出发后,骑行一段时间后与小军相距100 米,此时 小军骑行的时间为________分钟.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种子培育基地用A,B,C,D四种型号的小麦种子共2000粒进行发芽实验,从中选出发芽率高的种子进行推广.通过实验得知,C型号种子的发芽率为95%,根据实验数据绘制了图1和图2两幅尚不完整的统计图. 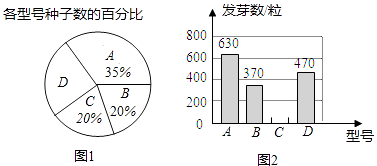
(1)D型号种子的粒数是粒;
(2)A型号种子的发芽率为;
(3)请你将图2的统计图补充完整;
(4)若将所有已发芽的种子放到一起,从中随机取出一粒,求取到B型号发芽种子的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是菱形ABCD对角线CA的延长线上任意一点,以线段AE为边作一个菱形AEFG,连接EB,GD.且∠DAB=∠EAG 
(1)求证:EB=GD;
(2)若∠DAB=60°,AB=2,AG= ![]() ,求GD的长.
,求GD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
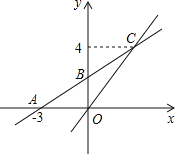
【题目】如图,在平面直角坐标系中,一次函数y=kx+b的图象与x轴交点为A(-3,0),与y轴交点为B,且与正比例函数![]() 的图象的交于点C(m,4).
的图象的交于点C(m,4).
(1)求m的值及一次函数y=kx+b的表达式;
(2)若点P是y轴上一点,且△BPC的面积为6,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某科技公司研发出一款多型号的智能手表,一家代理商出售该公司的A型智能手表去年销售总额为80000元,今年A型智能手表的售价每只比去年降低了600元,若售出的数量与去年相同,销售总额将比去年减少了25%.
(1)请问今年A型智能手表每只售价多少元?
(2)今年这家代理商准备新进一批A型智能手表和B型智能手表共100只,它们的进货价格与销售价格如表.若B型智能手表进货量不超过A型智能手表数量的3倍,所进智能手表可全部售完,请你设计出进货方案,使这批智能手表获利最多,并求出最大利润是多少元?
A型智能手表 | B型智能手表 | |
进价 | 1300元/只 | 1500元/只 |
售价 | 今年的售价 | 2300元/只 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com