
【题目】如图,点E是菱形ABCD对角线CA的延长线上任意一点,以线段AE为边作一个菱形AEFG,连接EB,GD.且∠DAB=∠EAG 
(1)求证:EB=GD;
(2)若∠DAB=60°,AB=2,AG= ![]() ,求GD的长.
,求GD的长.
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E在对角线AC上,点F在边BC上,连接BE、DF,DF交对角线AC于点G,且DE=DG. 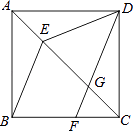
(1)求证:AE=CG;
(2)试判断BE和DF的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
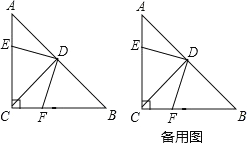
【题目】在△ABC 中,∠ACB=90°,AC=BC,D 是 AB 的中点,点 E 是边 AC 上的一动点,点F 是边 BC 上的一动点.
(1)若 AE=CF,试证明 DE=DF;
(2)在点 E、点 F 的运动过程中,若 DE⊥DF,试判断 DE 与 DF 是否一定相等? 并加以说明.
(3)在(2)的条件下,若 AC=2,四边形 ECFD 的面积是一个定值吗?若不是, 请说明理由,若是,请直接写出它的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在矩形ABCD中,∠ADC的平分线DE与BC边所在的直线交于点E,点P是线段DE上一定点(其中EP<PD)
(1)如图1,若点F在CD边上(不与D重合),将∠DPF绕点P逆时针旋转90°后,角的两边PD、PF分别交射线DA于点H、G.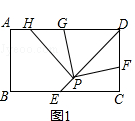
①求证:PG=PF; ②探究:DF、DG、DP之间有怎样的数量关系,并证明你的结论.
(2)拓展:如图2,若点F在CD的延长线上(不与D重合),过点P作PG⊥PF,交射线DA于点G,你认为(1)中DF、DG、DP之间的数量关系是否仍然成立?若成立,给出证明;若不成立,请写出它们所满足的数量关系式,并说明理由.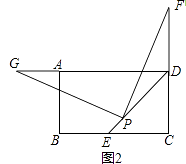
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】绵阳农科所为了考察某种水稻穗长的分布情况,在一块试验田里随机抽取了50个谷穗作为样本,量得它们的长度(单位:cm).对样本数据适当分组后,列出了如下频数分布表:
穗长 | 4.5≤x<5 | 5≤x<5.5 | 5.5≤x<6 | 6≤x<6.5 | 6.5≤x<7 | 7≤x<7.5 |
频数 | 4 | 8 | 12 | 13 | 10 | 3 |
(1)在图1、图2中分别出频数分布直方图和频数折线图;
(2)请你对这块试验田里的水稻穗长进行分析;并计算出这块试验田里穗长在5.5≤x<7范围内的谷穗所占的百分比.
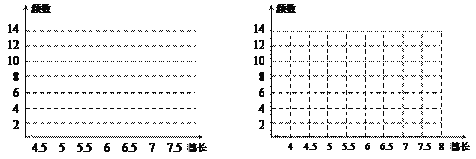
图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=m(x+1)(x﹣2)(m为常数,且m>0)与x轴从左至右依次交于A、B两点,与y轴交于点C,且OA=OC,经过点B的直线与抛物线的另一交点D在第二象限.
(1)求抛物线的函数表达式.
(2)若∠DBA=30°,设F为线段BD上一点(不含端点),连接AF,一动点M从点A出发,沿线段AF以每秒1个单位的速度运动到F,再沿线段FD以每秒2个单位的速度运动到D后停止,当点F的坐标是多少时,点M在整个运动过程中用时最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学生在素质教育基地进行社会实践活动,帮助农民伯伯采摘了黄瓜和茄子共40kg,了解到这些蔬菜的种植成本共42元,还了解到如下信息:

(1)请问采摘的黄瓜和茄子各多少千克?
(2)这些采摘的黄瓜和茄子可赚多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如何求tan75°的值?按下列方法作图可解决问题.如图,在Rt△ABC中,AC=k,∠ACB=90°,∠ABC=30°,延长CB至点M,在射线BM上截取线段BD,使BD=AB,连接AD.连接此图可求得tan75°的值为( )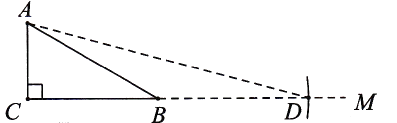
A.2- ![]()
B.2+ ![]()
C.1+ ![]()
D.![]()
-1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(探索新知)
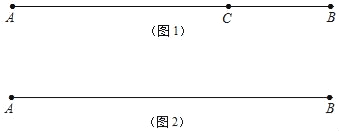
如图1,点C在线段AB上,图中共有3条线段:AB、AC和BC,若其中有一条线段的长度是另一条线段长度的两倍,则称点C是线段AB的“二倍点”.
(1)一条线段的中点 这条线段的“二倍点”;(填“是”或“不是”)
(深入研究)
如图2,若线段AB=20cm,点M从点B的位置开始,以每秒2cm的速度向点A运动,当点M到达点A时停止运动,运动的时间为t秒.
(2)问t为何值时,点M是线段AB的“二倍点”;
(3)同时点N从点A的位置开始,以每秒1cm的速度向点B运动,并与点M同时停止.请直接写出点M是线段AN的“二倍点”时t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com