
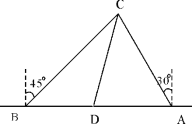
【题目】(本题满分9分)为了维护海洋权益,新组建的国家海洋局加大了在南海的巡逻力度。一天,我两艘海监船刚好在我某岛东西海岸线上的A、B两处巡逻,同时发现一艘不明国籍的船只停在C处海域。如图所示,AB=60![]() 海里,在B处测得C在北偏东45的方向上,A处测得C在北偏西30的方向上,在海岸线AB上有一灯塔D,测得AD=120
海里,在B处测得C在北偏东45的方向上,A处测得C在北偏西30的方向上,在海岸线AB上有一灯塔D,测得AD=120![]() 海里。
海里。
(1)(4分)分别求出A与C及B与C的距离AC,BC(结果保留根号)
(2)(5分)已知在灯塔D周围100海里范围内有暗礁群,我在A处海监船沿AC前往C处盘查,途中有无触礁的危险?(参考数据:![]() =1.41,
=1.41,![]() =1.73,
=1.73,![]() =2.45)
=2.45)
【答案】(1)AC=120![]() 海里 ,BC=120
海里 ,BC=120![]() 海里;(2)无触礁危险.
海里;(2)无触礁危险.
【解析】
试题分析:(1)过点C作CE⊥AB于E,解直角三角形即可求出A与C及B与C的距离AC,BC;(2)过点D作DF⊥AC于F,解直角三角形即可求出DF的长,再比较与100的大小,从而得出结论有无触礁的危险.
试题解析:⑴ 作CE⊥AB于E, 设AE=x
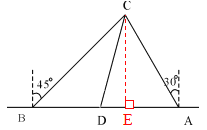
则在△ACE中,CE=![]() x AC=2 x
x AC=2 x
在△BCE中,BE=CE=![]() x BC=
x BC=![]() x
x
由AB=AE+BE ∴x+![]() x=60(
x=60(![]() +
+![]() )
)
解得x=60![]()
所以AC=120![]() (海里) ,BC=120
(海里) ,BC=120![]() (海里)
(海里)
⑵作DF⊥AC于F,
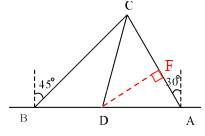
在△AFD中,DF=![]() DA
DA
∴DF=![]() ×60(
×60(![]() -
-![]() )=60(3
)=60(3![]() -
-![]() ) ≈106.8>100
) ≈106.8>100
所以无触礁危险.


 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案科目:初中数学 来源: 题型:
【题目】求解:已知:如图1,P为△ADC内一点,DP、CP分别平分DP、CP分别平分∠ADC和∠ACD。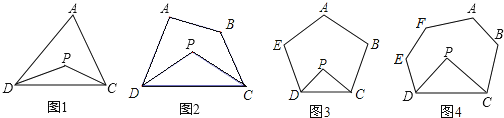
(1)如果∠A=60°,那么∠P是多少度;如果∠A=90°,那么∠P是多少度;如果∠A=x°,则∠P是多少度?
(2)如图2,P为四边形ABCD内一点,DP、CP分别平分∠ADC和∠BCD,试探究∠P与∠A+∠B的数量关系,并写出你的探索过程;
(3)如图3,P为五边形ABCDE内一点,DP、CP分别平分DP、CP分别平分∠ADC和∠ACD,请直接写出∠P与∠A+∠B+∠E的数量关系。
(4)如图4,P为六边形ABCDEF内一点,DP、CP分别平分DP、CP分别平分∠ADC和∠ACD,请直接写出∠P与∠A+∠B+∠E+∠F的数量关系。
(5)若P为n边形A1A2A3…An内一点,PA1平分∠AnA1A2 , PA2平分∠A1A2A3 , 请直接写出∠P与∠A3+A4+A5+…∠An的数量关系。(用含n的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC面积为1,第一次操作:分别延长AB,BC,CA至点A1 , B1 , C1 , 使A1B=AB,B1C=BC,C1A=CA,顺次连接A1 , B1 , C1 , 得到△A1B1C1 . 第二次操作:分别延长A1B1 , B1C1 , C1A1至点A2 , B2 , C2 , 使A2B1=A1B1 , B2C1=B1C1 , C2A1=C1A1 , 顺次连接A2 , B2 , C2 , 得到△A2B2C2 , …按此规律,要使得到的三角形的面积超过2010,最少经过( )次操作.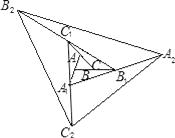
A.6
B.5
C.4
D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,BD是对角线,∠ABD=∠CDB,要使四边形ABCD是平行四边形只需添加一个条件,这个条件可以是____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标平面内,已点A(3,0)、B(﹣5,3),将点A向左平移6个单位到达C点,将点B向下平移6个单位到达D点. 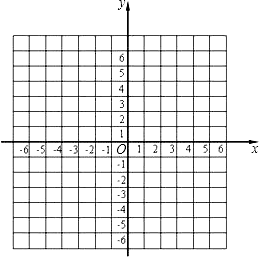
(1)写出C点、D点的坐标:C , D;
(2)把这些点按A﹣B﹣C﹣D﹣A顺次连接起来,这个图形的面积是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题8分)为深化义务教育课程改革,某校积极开展拓展性课程建设,设计开设艺术、体育、劳技、文学等多个类别的拓展性课程,要求每一位学生都自主选择一个类别的拓展性课程。为了了解学生选择拓展性课程的情况,随机抽取了部分学生进行调查,并将调查结果绘制成如下统计图(部分信息未给出):
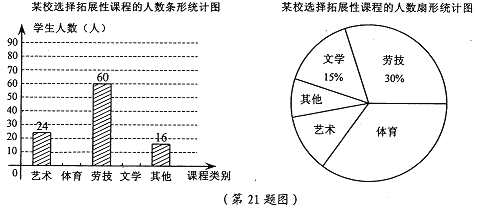
根据统计图中的信息,解答下列问题:
(1)求本次被调查的学生人数;
(2)将条形图补充完整;
(3)若该校共有1600名学生,请估计全校选择体育类的学生人数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD,动点E在AC上,AF⊥AC,垂足为A,AF=AE. 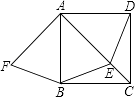
(1)求证:BF=DE;
(2)当点E运动到AC中点时(其他条件都保持不变),问四边形AFBE是什么特殊四边形?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com