
【题目】求解:已知:如图1,P为△ADC内一点,DP、CP分别平分DP、CP分别平分∠ADC和∠ACD。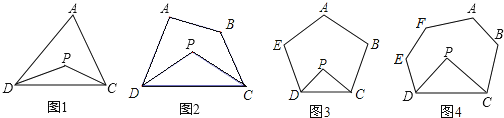
(1)如果∠A=60°,那么∠P是多少度;如果∠A=90°,那么∠P是多少度;如果∠A=x°,则∠P是多少度?
(2)如图2,P为四边形ABCD内一点,DP、CP分别平分∠ADC和∠BCD,试探究∠P与∠A+∠B的数量关系,并写出你的探索过程;
(3)如图3,P为五边形ABCDE内一点,DP、CP分别平分DP、CP分别平分∠ADC和∠ACD,请直接写出∠P与∠A+∠B+∠E的数量关系。
(4)如图4,P为六边形ABCDEF内一点,DP、CP分别平分DP、CP分别平分∠ADC和∠ACD,请直接写出∠P与∠A+∠B+∠E+∠F的数量关系。
(5)若P为n边形A1A2A3…An内一点,PA1平分∠AnA1A2 , PA2平分∠A1A2A3 , 请直接写出∠P与∠A3+A4+A5+…∠An的数量关系。(用含n的代数式表示)
【答案】
(1)
解答:∵DP、CP分别平分∠ADC和∠ACD,
∴∠PDC= ![]() ∠ADC,∠PCD=
∠ADC,∠PCD= ![]() ∠ACD,
∠ACD,
∴∠DPC=180°-∠PDC-∠PCD=180°- ![]() (∠ADC+∠ACD)=180°-
(∠ADC+∠ACD)=180°- ![]() (180°-∠A)
(180°-∠A)
=90°+ ![]() ∠A,
∠A,
∴如果∠A=60°,那么∠P=120°;如果∠A=90°,那么∠P=135°;如果∠A=x°,则∠P=(90+ ![]() )°
)°
(2)
解答: ∵DP、CP分别平分∠ADC和∠BCD,
∴∠PDC= ![]() ∠ADC,∠PCD=
∠ADC,∠PCD= ![]() ∠BCD,
∠BCD,
∴∠DPC=180°-∠PDC-∠PCD=180°- ![]() (∠ADC+∠BCD)=180°-
(∠ADC+∠BCD)=180°- ![]() (360°-∠A-∠B)
(360°-∠A-∠B)
= ![]() (∠A+∠B);
(∠A+∠B);
(3)
解答:五边形ABCDEF的内角和为:(5-2)180°=540°,
∵DP、CP分别平分∠EDC和∠BCD,
∴∠P= ![]() ∠EDC,∠PCD=
∠EDC,∠PCD= ![]() ∠BCD,
∠BCD,
∴∠P=180°-∠PDC-∠PCD=180°- ![]() (∠EDC+∠BCD)=180°-
(∠EDC+∠BCD)=180°- ![]() (540°-∠A-∠B-∠E)
(540°-∠A-∠B-∠E)
= ![]() (∠A+∠B+∠E)-90°.
(∠A+∠B+∠E)-90°.
(4)
解答:六边形ABCDEF的内角和为:(6-2)180°=720°,
∵DP、CP分别平分∠EDC和∠BCD,
∴∠PDC= ![]() ∠EDC,∠PCD=
∠EDC,∠PCD= ![]() ∠BCD,
∠BCD,
∴∠P=180°-∠PDC-∠PCD=180°- ![]() (∠EDC+∠BCD)=180°-
(∠EDC+∠BCD)=180°- ![]() (720°-∠A-∠B-∠E-∠F)=
(720°-∠A-∠B-∠E-∠F)= ![]() (∠A+∠B+∠E+∠F)-180°.
(∠A+∠B+∠E+∠F)-180°.
(5)
解答:同第一小题可得,∠P= ![]() (∠A3+∠A4+∠A5+…∠An)-(n-4)×90°.
(∠A3+∠A4+∠A5+…∠An)-(n-4)×90°.
【解析】这五小题的做法类似,把求∠P的度数转换成求 ![]() (∠EDC+∠BCD),由多边形的内角和可得(∠EDC+∠BCD)与其他内角和的数量关系,从而得∠P.
(∠EDC+∠BCD),由多边形的内角和可得(∠EDC+∠BCD)与其他内角和的数量关系,从而得∠P.
【考点精析】认真审题,首先需要了解多边形内角与外角(多边形的内角和定理:n边形的内角和等于(n-2)180°.多边形的外角和定理:任意多边形的外角和等于360°).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知AM∥BN,∠A=60°.点P是射线AM上一动点(与点A不重合),  BC、BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
BC、BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)求∠CBD的度数;
(2)当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律.
(3)当点P运动到使∠ACB=∠ABD时,∠ABC的度数是?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角坐标系中,△ABC的顶点都在网格点上.其中,A点坐标为(2, ﹣1),将△ABC向右平移3个单位,再向下平移2个单位得到△A1B1C1 , 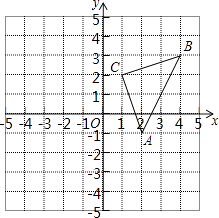
(1)画出平移后的图形;
(2)写出A1、B1、C1的坐标;、
(3)求△A1B1C1的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个多边形纸片按图示的剪法剪去一个内角后,得到一个内角和为2340°的新多边形,则原多边形的对角线条数为( ) 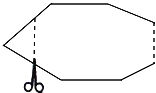
A.77
B.90
C.65
D.104
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设A(﹣2,y1),B(1,y2),C(2,y3)是抛物线y=3(x+1)2+4m(m为常数)上的三点,则y1,y2,y3的大小关系为( )
A.y1<y2<y3B.y2<y1<y3C.y3<y1<y2D.y3<y2<y1
查看答案和解析>>
科目:初中数学 来源: 题型:
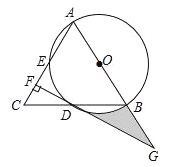
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交线段BC,AC于点D,E,过点D作DF⊥AC,垂足为F,线段FD,AB的延长线相交于点G.
(1)求证:DF是⊙O的切线;
(2)若CF=1,DF=![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
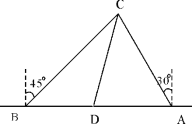
【题目】(本题满分9分)为了维护海洋权益,新组建的国家海洋局加大了在南海的巡逻力度。一天,我两艘海监船刚好在我某岛东西海岸线上的A、B两处巡逻,同时发现一艘不明国籍的船只停在C处海域。如图所示,AB=60![]() 海里,在B处测得C在北偏东45的方向上,A处测得C在北偏西30的方向上,在海岸线AB上有一灯塔D,测得AD=120
海里,在B处测得C在北偏东45的方向上,A处测得C在北偏西30的方向上,在海岸线AB上有一灯塔D,测得AD=120![]() 海里。
海里。
(1)(4分)分别求出A与C及B与C的距离AC,BC(结果保留根号)
(2)(5分)已知在灯塔D周围100海里范围内有暗礁群,我在A处海监船沿AC前往C处盘查,途中有无触礁的危险?(参考数据:![]() =1.41,
=1.41,![]() =1.73,
=1.73,![]() =2.45)
=2.45)
查看答案和解析>>
科目:初中数学 来源: 题型:
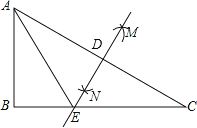
【题目】如图,在Rt△ABC中,∠B=90°,分别以A、C为圆心,大于![]() AC长为半径画弧,两弧相交于点M、N,连结MN,与AC、BC分别交于点D、E,连结AE,则:
AC长为半径画弧,两弧相交于点M、N,连结MN,与AC、BC分别交于点D、E,连结AE,则:
(1)∠ADE= ;
(2)AE EC;(填“=”“>”或“<”)
(3)当AB=3,AC=5时,△ABE的周长=
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com