
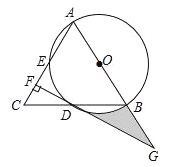
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交线段BC,AC于点D,E,过点D作DF⊥AC,垂足为F,线段FD,AB的延长线相交于点G.
(1)求证:DF是⊙O的切线;
(2)若CF=1,DF=![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
【答案】(1)详见解析;(2)
【解析】
试题分析:(1)连接AD、OD,由AB为直径可得出点D为BC的中点,由此得出OD为△BAC的中位线,再根据中位线的性质即可得出OD⊥DF,从而证出DF是⊙O的切线;(2)CF=1,DF=![]() ,通过解直角三角形得出CD=2、∠C=60°,从而得出△ABC为等边三角形,再利用分割图形求面积法即可得出阴影部分的面积.
,通过解直角三角形得出CD=2、∠C=60°,从而得出△ABC为等边三角形,再利用分割图形求面积法即可得出阴影部分的面积.
试题解析:(1)证明:连接AD、OD,如图所示.
∵AB为直径,
∴∠ADB=90°,
∴AD⊥BC,
∵AC=AB,
∴点D为线段BC的中点.
∵点O为AB的中点,
∴OD为△BAC的中位线,
∴OD∥AC,
∵DF⊥AC,
∴OD⊥DF,
∴DF是⊙O的切线.
(2)解:在Rt△CFD中,CF=1,DF=![]() ,
,
∴tan∠C=![]() =
=![]() ,CD=2,
,CD=2,
∴∠C=60°,
∵AC=AB,
∴△ABC为等边三角形,
∴AB=4.
∵OD∥AC,
∴∠DOG=∠BAC=60°,
∴DG=ODtan∠DOG=2![]() ,
,
∴S阴影=S△ODG﹣S扇形OBD=![]() DGOD﹣
DGOD﹣![]() πOB2=2
πOB2=2![]() ﹣
﹣![]() π.
π.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,直线EF与AB,CD分别交于点M,N,过点N的直线GH与AB交于点P,则下列结论错误的是( ) 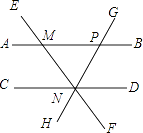
A.∠EMB=∠END
B.∠BMN=∠MNC
C.∠CNH=∠BPG
D.∠DNG=∠AME
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】求解:已知:如图1,P为△ADC内一点,DP、CP分别平分DP、CP分别平分∠ADC和∠ACD。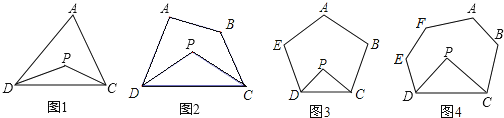
(1)如果∠A=60°,那么∠P是多少度;如果∠A=90°,那么∠P是多少度;如果∠A=x°,则∠P是多少度?
(2)如图2,P为四边形ABCD内一点,DP、CP分别平分∠ADC和∠BCD,试探究∠P与∠A+∠B的数量关系,并写出你的探索过程;
(3)如图3,P为五边形ABCDE内一点,DP、CP分别平分DP、CP分别平分∠ADC和∠ACD,请直接写出∠P与∠A+∠B+∠E的数量关系。
(4)如图4,P为六边形ABCDEF内一点,DP、CP分别平分DP、CP分别平分∠ADC和∠ACD,请直接写出∠P与∠A+∠B+∠E+∠F的数量关系。
(5)若P为n边形A1A2A3…An内一点,PA1平分∠AnA1A2 , PA2平分∠A1A2A3 , 请直接写出∠P与∠A3+A4+A5+…∠An的数量关系。(用含n的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC面积为1,第一次操作:分别延长AB,BC,CA至点A1 , B1 , C1 , 使A1B=AB,B1C=BC,C1A=CA,顺次连接A1 , B1 , C1 , 得到△A1B1C1 . 第二次操作:分别延长A1B1 , B1C1 , C1A1至点A2 , B2 , C2 , 使A2B1=A1B1 , B2C1=B1C1 , C2A1=C1A1 , 顺次连接A2 , B2 , C2 , 得到△A2B2C2 , …按此规律,要使得到的三角形的面积超过2010,最少经过( )次操作.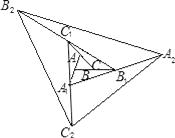
A.6
B.5
C.4
D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标平面内,已点A(3,0)、B(﹣5,3),将点A向左平移6个单位到达C点,将点B向下平移6个单位到达D点. 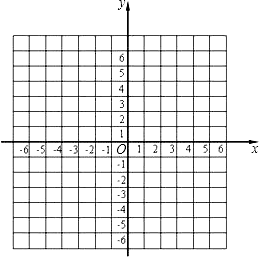
(1)写出C点、D点的坐标:C , D;
(2)把这些点按A﹣B﹣C﹣D﹣A顺次连接起来,这个图形的面积是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把三张大小相同的正方形卡片A、B、C叠放在一个底面为正方形的盒底上,底面未被卡片覆盖的部分用阴影表示,若按图1摆放时,阴影部分的面积为S1;若按图2摆放时,阴影部分的面积为S2 , 则S1与S2的大小关系是( )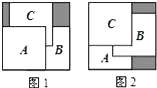
A.S1>S2
B.S1<S2
C.S1=S2
D.无法确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com