
【题目】在平面直角坐标系xOy中,对于双曲线y= ![]() (m>0)和双曲线y=
(m>0)和双曲线y= ![]() (n>0),如果m=2n,则称双曲线y=
(n>0),如果m=2n,则称双曲线y= ![]() (m>0)和双曲线y=
(m>0)和双曲线y= ![]() (n>0)为“倍半双曲线”,双曲线y=
(n>0)为“倍半双曲线”,双曲线y= ![]() (m>0)是双曲线y=
(m>0)是双曲线y= ![]() (n>0)的“倍双曲线”,双曲线y=
(n>0)的“倍双曲线”,双曲线y= ![]() (n>0)是双曲线y=
(n>0)是双曲线y= ![]() (m>0)的“半双曲线”,
(m>0)的“半双曲线”,
(1)请你写出双曲线y= ![]() 的“倍双曲线”是;双曲线y=
的“倍双曲线”是;双曲线y= ![]() 的“半双曲线”是;
的“半双曲线”是;
(2)如图1,在平面直角坐标系xOy中,已知点A是双曲线y= ![]() 在第一象限内任意一点,过点A与y轴平行的直线交双曲线y=
在第一象限内任意一点,过点A与y轴平行的直线交双曲线y= ![]() 的“半双曲线”于点B,求△AOB的面积;
的“半双曲线”于点B,求△AOB的面积;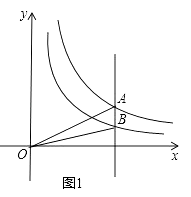
(3)如图2,已知点M是双曲线y= ![]() (k>0)在第一象限内任意一点,过点M与y轴平行的直线交双曲线y=
(k>0)在第一象限内任意一点,过点M与y轴平行的直线交双曲线y= ![]() 的“半双曲线”于点N,过点M与x轴平行的直线交双曲线y=
的“半双曲线”于点N,过点M与x轴平行的直线交双曲线y= ![]() 的“半双曲线”于点P,若△MNP的面积记为S△MNP , 且1≤S△MNP≤2,求k的取值范围.
的“半双曲线”于点P,若△MNP的面积记为S△MNP , 且1≤S△MNP≤2,求k的取值范围.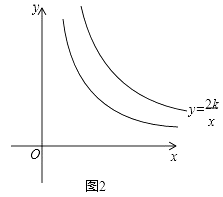
【答案】
(1)y= ![]() ;y=
;y= ![]()
(2)
解:如图1,
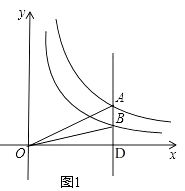
∵双曲线y= ![]() 的“半双曲线”是y=
的“半双曲线”是y= ![]() ,
,
∴△AOD的面积为2,△BOD的面积为1,
∴△AOB的面积为1
(3)
解:解法一:如图2,
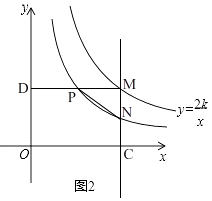
依题意可知双曲线 ![]() 的“半双曲线”为
的“半双曲线”为 ![]() ,
,
设点M的横坐标为m,则点M坐标为(m, ![]() ),点N坐标为(m,
),点N坐标为(m, ![]() ),
),
∴CM= ![]() ,CN=
,CN= ![]() .
.
∴MN= ![]() ﹣
﹣ ![]() =
= ![]() .
.
同理PM=m﹣ ![]() =
= ![]() .
.
∴S△PMN= ![]() MNPM=
MNPM= ![]()
∵1≤S△PMN≤2,
∴1≤ ![]() ≤2.
≤2.
∴4≤k≤8,
解法二:如图3,
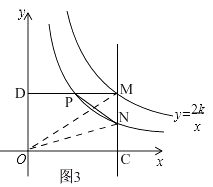
依题意可知双曲线 ![]() 的“半双曲线”为
的“半双曲线”为 ![]() ,
,
设点M的横坐标为m,则点M坐标为(m, ![]() ),点N坐标为(m,
),点N坐标为(m, ![]()
∴点N为MC的中点,同理点P为MD的中点.
连接OM,
∵ ![]() ,
,
∴△PMN∽△OCM.
∴ ![]() .
.
∵S△OCM=k,
∴S△PMN= ![]() .
.
∵1≤S△PMN≤2,
∴1≤ ![]() ≤2.
≤2.
∴4≤k≤8.
【解析】解:(1)由“倍双曲线”的定义
∴双曲线y= ![]() ,的“倍双曲线”是y=
,的“倍双曲线”是y= ![]() ;
;
双曲线y= ![]() 的“半双曲线”是y=
的“半双曲线”是y= ![]() .
.
所以答案是y= ![]() ,y=
,y= ![]() ;
;
【考点精析】掌握反比例函数的概念和反比例函数的图象是解答本题的根本,需要知道形如y=k/x(k为常数,k≠0)的函数称为反比例函数.自变量x的取值范围是x不等于0的一切实数,函数的取值范围也是一切非零实数;反比例函数的图像属于双曲线.反比例函数的图象既是轴对称图形又是中心对称图形.有两条对称轴:直线y=x和 y=-x.对称中心是:原点.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】如图在平面直角坐标系中,△ABC各顶点的坐标分别为:A(4,0),B(﹣1,4),C(﹣3,1)
(1)在图中作△A′B′C′使△A′B′C′和△ABC关于x轴对称;
(2)写出点A′B′C′的坐标;
(3)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三角板是学习数学的重要工具,将一副三角板中的两块直角三角板的直角顶点![]() 按如图方式叠放在一起,当
按如图方式叠放在一起,当![]() 且点
且点![]() 在直线
在直线![]() 的上方时,解决下列问题:(友情提示:
的上方时,解决下列问题:(友情提示:![]() ,
,![]() ,
,![]() .
.

(1)①若![]() ,则
,则![]() 的度数为 ;
的度数为 ;
②若![]() ,则
,则![]() 的度数为 ;
的度数为 ;
(2)由(1)猜想![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
(3)这两块三角板是否存在一组边互相平行?若存在,请直接写出![]() 的角度所有可能的值(不必说明理由);若不存在,请说明理由.
的角度所有可能的值(不必说明理由);若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
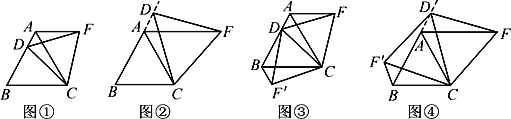
【题目】(1)操作发现:如图①,D是等边△ABC的边BA上一动点(点D与点B不重合),连接DC,以DC为边在BC上方作等边△DCF,连接AF,你能发现AF与BD之间的数量关系吗?并证明你发现的结论;
(2)类比猜想:如图②,当动点D运动至等边△ABC边BA的延长线时,其他作法与(1)相同,猜想AF与BD在(1)中的结论是否仍然成立?
(3)深入探究:Ⅰ.如图③,当动点D在等边△ABC边BA上运动时(点D与B不重合),连接DC,以DC为边在BC上方和下方分别作等边△DCF和等边△DCF′,连接AF,BF′,探究AF,BF′与AB有何数量关系?并证明你的探究的结论;Ⅱ.如图④,当动点D在等边△ABC的边BA的延长线上运动时,其他作法与图③相同,Ⅰ中的结论是否成立?若不成立,是否有新的结论?并证明你得出的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
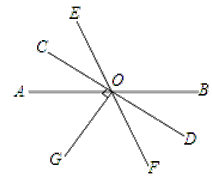
【题目】如图,已知直线AB、CD、EF相交于点O,OG⊥CD,∠BOD=36°.
(1)求∠AOG的度数;
(2)若OG是∠AOF的平分线,那么OC是∠AOE的平分线吗?说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司到果园基地购买某种优质水果,慰问医务工作者,果园基地对购买量在3000千克以上(含3000千克)的有两种销售方案,甲方案:每千克9元,由基地送货上门.乙方案:每千克8元,由顾客自己租车运回,已知该公司租车从基地到公司的运输费为5000元.
(1)分别写出该公司两种购买方案的付款y(元)与所购买的水果质量x(千克)之间的函数关系式,并写出自变量x的取值范围.
(2)依据购买量判断,选择哪种购买方案付款最少?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某“数学兴趣小组”根据学习函数的经验,对函数y= ![]() 的图象和性质进行了探究,探究过程如下,请补充完整:
的图象和性质进行了探究,探究过程如下,请补充完整: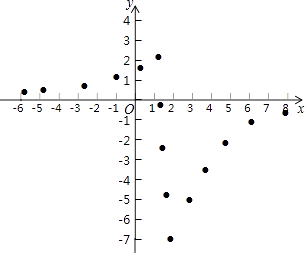
(1)该函数的自变量x的取值范围是;
(2)同学们先找到y与x的几组对应值,然后在下图的平面直角坐标系xOy中,描出各对对应值为坐标的点.请你根据描出的点,画出该函数的图象;
(3)结合画出的函数图象,写出该函数的一条性质: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x、y的方程组![]() 给出下列结论:①
给出下列结论:①![]() 是方程组的解;②无论a取何值,x,y的值都不可能互为相反数;③当a=1时,方程组的解也是方程x+y=4-a的解;④x,y都为自然数的解有4对.其中正确的个数为( )
是方程组的解;②无论a取何值,x,y的值都不可能互为相反数;③当a=1时,方程组的解也是方程x+y=4-a的解;④x,y都为自然数的解有4对.其中正确的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com